Scheduling theory
A branch of applied mathematics (a division of operations research) concerned with mathematical formulations and solution methods of problems of optimal ordering and coordination in time of certain operations. Scheduling theory includes questions on the development of optimal schedules (Gantt charts, graphs) for performing finite (or repetitive) sets of operations. The area of application of results in scheduling theory include management, production, transportation, computer systems, construction, etc.
The problems that scheduling theory deals with are usually formulated as optimization problems for a process of processing a finite set of jobs in a system with limited resources. A finite set of jobs is what distinguishes scheduling models from similar models in queueing theory, where basically infinite flows of activities are considered. In all other respects the starting points of the two theories are close. In scheduling theory, the time of arrival for every job into the system is specified. Within the system the job has to pass several processing stages, depending on the conditions of the problem. For every stage, feasible sets of resources are given, as well as the processing time depending on the resources used. The possibility of interruptions in the processing of certain jobs (so-called pre-emptions) can also be stipulated. Constraints on the processing sequence are usually described by a transitive anti-reflexive binary relation. Algorithms for the evaluation of characteristics of large partially ordered sets of jobs constitute the essence of the part of scheduling theory called network analysis (cf. Network model; Network planning). Sometimes, in scheduling models durations of re-adjustments are specified that are necessary when one job in process is replaced by another, as well as certain other conditions.
It should be mentioned that, being practically oriented, scheduling theory does not seek to unify its terminology; along with the term "job" , terms like "task" , "operation" , etc., are also used. For the same reason a processing schedule is formally defined in several ways. In the general case, a schedule can be understood as a single-valued mapping that to every job at every moment assigns a certain set of resources. As criteria, total and maximal costs of the form
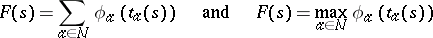 |
are usually taken, where  is the completion time of job
is the completion time of job  according to schedule
according to schedule  ,
, 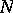 is the set of all jobs and the
is the set of all jobs and the 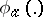 are non-decreasing functions, called cost functions. In practical formulations the cost functions usually have a specific economical meaning (like freezing floating capital, damages by loss of customers, etc.). Multi-criterion problems are also considered.
are non-decreasing functions, called cost functions. In practical formulations the cost functions usually have a specific economical meaning (like freezing floating capital, damages by loss of customers, etc.). Multi-criterion problems are also considered.
In addition to deterministic models, stochastic models are also studied. In this case either the minimization problem for the expectation of one of the criteria used in a deterministic formulation is considered, or the probability of a certain event is minimized. Such an event can be, e.g., a delay in processing relative to described terms.
The basic approach to the solution of deterministic scheduling problems is the general algorithmic scheme of enumerative optimization (branch-and-bound). In this way most practical problems were successfully solved, and optimization procedures for the planning of jobs in time were developed (calendar planning). These have been realized in automatic control systems. Along with that, fast decision rules for a number of specific deterministic problems were obtained, necessary and sufficient conditions for their use were proved, and effective methods were proposed that are important for general discrete optimization problems (see [1]–[4]). Results from graph theory and mathematical programming are often applicable to the development of optimization algorithms of this kind. Work on  -completeness published at the beginning of the 1970's stimulated numerous studies on the complexity of scheduling problems (see, e.g., [5]). The results of this research enhanced the interest in approximation algorithms and bounds on their performance (see, e.g., [6]). Scheduling presents easily formulated and practically meaningful problems, which are "touchstones" for many approaches and methods of discrete optimization.
-completeness published at the beginning of the 1970's stimulated numerous studies on the complexity of scheduling problems (see, e.g., [5]). The results of this research enhanced the interest in approximation algorithms and bounds on their performance (see, e.g., [6]). Scheduling presents easily formulated and practically meaningful problems, which are "touchstones" for many approaches and methods of discrete optimization.
References
| [1] | V.S. Tanaev, V.V. Shkurba, "Introduction to scheduling theory" , Moscow (1975) (In Russian) |
| [2] | R.W. Conway, W.L. Maxwell, L.W. Miller, "Theory of scheduling" , Addison-Wesley (1967) |
| [3] | J.L. Bruno (ed.) et al. (ed.) , Computer and job-shop scheduling theory , Wiley (1976) |
| [4] | M.J. Gonzalez, "Deterministic processor scheduling" Comput. Surveys , 9 : 3 (1977) pp. 173–204 |
| [5] | J.K. Lenstra, A.H.G. Rinnooy Kan, "Complexity of scheduling under precedence constraints" Operations Research , 26 : 1 (1978) pp. 22–35 |
| [6] | M.R. Garey, R.L. Graham, D.S. Johnson, "Performance guarantees for scheduling algorithms" Operations Research , 26 : 1 (1978) pp. 3–21 |
Comments
Scheduling problems have become the subject of systematic mathematical research since the mid-1950s, starting with the pioneering work of S.M. Johnson [a1], W.E. Smith [a2], and G.B. Dantzig, D.R. Fulkerson and S.M. Johnson [a3], which was devoted to three scheduling problems that have become classical in contemporary scheduling theory and operations research. These were: the multi-machine flowshop minimum-completion-time scheduling problem, the single-machine minimum-total-weighted-completion-time scheduling problem and the travelling-salesman problem.
Complexity.
These three problems, like many other scheduling problems that were investigated in the next  years, have been shown to possess the following property of computational intractability: While some of their simplified variants can be solved efficiently, i.e., in a polynomial number of computational steps, these problems, in general, defy exact solution in polynomial time, the latter meaning that all methods currently known for their (exact) solution can, in the worst case, blow up exponentially in the problem size.
years, have been shown to possess the following property of computational intractability: While some of their simplified variants can be solved efficiently, i.e., in a polynomial number of computational steps, these problems, in general, defy exact solution in polynomial time, the latter meaning that all methods currently known for their (exact) solution can, in the worst case, blow up exponentially in the problem size.
It is a key question in scheduling theory and, more generally, in combinatorial optimization theory, if any of these problems can be solved in polynomial time. Fundamental work by S.A. Cook [a4], R.M. Karp [a5] and L.A. Levin [a6] has provided strong evidence in favour of the negative answer to this question. Their theory of computational complexity of combinatorial problems has introduced the concept of 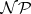 -hardness. While omitting formal details of the corresponding definition (which can be found in [a4]–[a7]), it is here observed that the class of
-hardness. While omitting formal details of the corresponding definition (which can be found in [a4]–[a7]), it is here observed that the class of 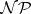 -hard problems contains the three scheduling problems above, as well as literally thousands of other combinatorial problems, and possesses two important properties. First, all these problems have the above-mentioned property of computational intractability. Secondly, if any particular
-hard problems contains the three scheduling problems above, as well as literally thousands of other combinatorial problems, and possesses two important properties. First, all these problems have the above-mentioned property of computational intractability. Secondly, if any particular 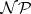 -hard problem would have a polynomial-time algorithm for solving it, then all of them would. It is strongly believed (but has not yet (1991) been proved) that no such algorithm exists. More details on the complexity theory of scheduling problems can be found in [a7]–[a10]; related material is discussed in Complexity theory.
-hard problem would have a polynomial-time algorithm for solving it, then all of them would. It is strongly believed (but has not yet (1991) been proved) that no such algorithm exists. More details on the complexity theory of scheduling problems can be found in [a7]–[a10]; related material is discussed in Complexity theory.
Problem statement.
In attempts to bring some order in the large variety of scheduling problems, several general frameworks for their description and classification have been suggested (see, e.g., [1]–[5], [a8]–[a11]). One such framework ([a10], [a11]) is briefly presented below.
One considers three sets: a set of  jobs (or "tasks" , "operations" or "activities" ), a set of
jobs (or "tasks" , "operations" or "activities" ), a set of 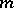 machines (or "processors" , "operators" or "robots" ) and a set of
machines (or "processors" , "operators" or "robots" ) and a set of  resources, other than machines, needed for processing the jobs.
resources, other than machines, needed for processing the jobs.
There is given a directed graph, or a network, in which the nodes correspond to jobs while arcs depict precedence relations between jobs, meaning that some jobs may be started (finished) only after some other jobs are started (finished).
For each job 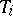 , one knows the arrival time (the time at which
, one knows the arrival time (the time at which 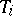 is ready for processing), a deadline (the time at which
is ready for processing), a deadline (the time at which 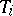 must be completed) and "preferred intervals" , the starting (finishing) of the job outside of which, either "too early or too late" , is discouraged by imposing corresponding penalties.
must be completed) and "preferred intervals" , the starting (finishing) of the job outside of which, either "too early or too late" , is discouraged by imposing corresponding penalties.
For each ordered pair of jobs 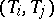 one knows also the lower and upper bounds on the "time shifts" between the start (finish) of the job
one knows also the lower and upper bounds on the "time shifts" between the start (finish) of the job 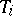 and that of
and that of 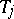 .
.
Along with that, for each job 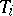 one knows a finite set
one knows a finite set 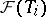 of "feasible variants" of performing it; each of the variants
of "feasible variants" of performing it; each of the variants 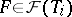 is represented by its list of required resources together with the related processing time
is represented by its list of required resources together with the related processing time 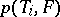 . No two jobs demanding the same resource can be processed simultaneously.
. No two jobs demanding the same resource can be processed simultaneously.
A schedule is defined as a pair of functions on the set of jobs, 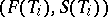 ,
, 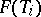 being a uniquely chosen feasible variant for performing the job
being a uniquely chosen feasible variant for performing the job 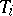 and
and 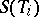 being the starting time of job
being the starting time of job 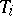 .
.
The problem is to find the schedule satisfying all arrival/deadline and resource constraints, while minimizing (or maximizing) a chosen optimality criterion.
The general scheduling problem described above includes thousands of possible variations.
Permitting its components (the input data, constraints and criterion) to be either deterministic or probabilistic, one can obtain various deterministic or stochastic scheduling problems; for deterministic problems see, e.g., [1]–[6], [a8]–[a11]; for stochastic problems see, e.g., [a12]–[a13].
By specifying practical aspects of the model above one can obtain problem formulations in terms of machine-scheduling, time tabling, project scheduling or periodic scheduling in production, transportation or computer systems ([1]–[4], [a8]–[a13]).
By specifying a machine environment one readily obtains scheduling problems for a single machine, parallel machines or sequential machines of various types: flowshop, jobshop or open shop. Along with that one can choose job characteristics (e.g., pre-emption allowed or not, precedence constraints given or not, release deadlines/dates arbitrary or equal, etc.) and, also, specify the optimality criterion, scalar or vectorial, as a function (respectively, vector-function) of the start/finish times of the jobs as well as of the resource allocation (maximum completion time, total completion time, total penalty for earliness/tardiness, etc.) (see, e.g., [a8]–[a13] for further details).
As an illustration of the diversity of scheduling problems, three special cases of the general model above are now described; these are also the three scheduling problems referred to above.
The travelling-salesman problem.
To find the shortest route that visits each of a given collection of  cities and finally returns to the city from which it started. A reformulation of this problem in terms of machine-scheduling ( "cities" becoming machines and "distances" between cities becoming the set-up times) is evident.
cities and finally returns to the city from which it started. A reformulation of this problem in terms of machine-scheduling ( "cities" becoming machines and "distances" between cities becoming the set-up times) is evident.
The single-machine problem.
(Smith's problem.) A set of  jobs is to be processed on a single machine. The machine is available at time zero, and pre-emption of jobs is not allowed. The
jobs is to be processed on a single machine. The machine is available at time zero, and pre-emption of jobs is not allowed. The  -th job is characterized by its processing time,
-th job is characterized by its processing time, 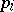 , and a "weight"
, and a "weight" 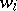 determining its priority. In the general case the precedence relations between the jobs are specified. The problem is to find an order
determining its priority. In the general case the precedence relations between the jobs are specified. The problem is to find an order 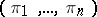 of jobs minimizing the total weighted completion time:
of jobs minimizing the total weighted completion time:
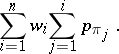 |
In the special case when the jobs have no precedence relations specified (actually, this is the case considered by Smith [a2]), the following Smith rule solves the problem: any sequence putting the jobs in order of non-decreasing ratios 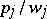 is optimal, [a2]. Adding arbitrary precedence constraints between jobs results in
is optimal, [a2]. Adding arbitrary precedence constraints between jobs results in  -hardness, [5], [a14], and the same happens as soon as arbitrary arrival dates or deadlines are added to the model [a15].
-hardness, [5], [a14], and the same happens as soon as arbitrary arrival dates or deadlines are added to the model [a15].
The multi-machine flowshop problem.
(Johnson's problem.) A system of 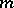 machines is given to process sequentially
machines is given to process sequentially  jobs
jobs 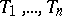 , in the same order for all jobs, say,
, in the same order for all jobs, say, 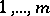 . For each job
. For each job  one knows the processing time
one knows the processing time 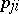 on machine
on machine 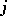 (
(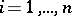 ;
;  ). Each job may start processing on machine
). Each job may start processing on machine 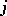 not before its completion on machine
not before its completion on machine 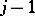 ; each machine processes a job without interruption; each machine can process at most one job at a time, and each job can be processed on at most one machine at a time; buffer capacities are provided for storage of work-in-process.
; each machine processes a job without interruption; each machine can process at most one job at a time, and each job can be processed on at most one machine at a time; buffer capacities are provided for storage of work-in-process.
It is required to determine, for each machine, the job processing sequence so as to minimize the completion time of all jobs on all machines.
In the case of two machines, the following Johnson rule solves the problem in 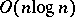 steps: Any sequence that puts the jobs in the same order for both machines, first the jobs having
steps: Any sequence that puts the jobs in the same order for both machines, first the jobs having 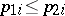 in order of non-decreasing
in order of non-decreasing 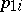 and then the remaining jobs in order of non-increasing
and then the remaining jobs in order of non-increasing 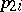 is optimal, [a1].
is optimal, [a1].
If the number of machines 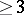 , the Johnson problem becomes
, the Johnson problem becomes 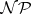 -hard.
-hard.
Mathematical methods of scheduling theory.
As in discrete optimization (see Integer programming), the mathematical methods in scheduling theory can be divided into specialized ones (which are capable of solving only restricted classes or only individual problems) and general ones (i.e., those intended for the solution of wide classes of discrete optimization problems).
Among the algorithms of the first group the most celebrated are: i) the "listing" algorithms, which are a special subfamily of local search methods of discrete optimization, well adjusted to the specificity of scheduling problems; ii) the "interchange technique" , which is a subclass of the listing algorithms and a good adaptation to scheduling of gradient-type methods; and iii) unique combinatorial algorithms, which cannot be extended even to solving "very similar" problems, such as, e.g., the Gilmore–Gomory algorithm, , for solving a special case of the travelling-salesman problem. A number of specialized algorithms is presented in books and surveys, [a7]–[a13].
Algorithms of the second group, the general ones, are, in essence, the traditional computational methods of discrete optimization. They are divided into deterministic and probabilistic; exact and approximate. The most celebrated are: branch-and-bound, dynamic programming, linear programming relaxation, Lagrangian relaxation, polyhedral analysis, local search (see, e.g., the books [a17]–[a18] on combinatorial optimization; related material can be found in Integer programming; Operations research; Project management and scheduling, mathematical theory of).
The area of scheduling serves as a testing ground for new mathematical ideas of discrete optimization, decision-making system design and artificial intelligence.
References
| [a1] | S.M. Johnson, "Optimal two- and three-stage production schedules with setup times included" Naval Res. Logist. Quart. , 1 (1954) pp. 61–68 |
| [a2] | W.E. Smith, "Various optimizers for single-stage production" Naval Res. Logist. Quart. , 23 (481–486) |
| [a3] | G.B. Dantzig, D.R. Fulkerson, S.M. Johnson, "Solution of a large-scale traveling-salesman problem" Oper. Res. , 2 (1954) pp. 393–410 |
| [a4] | S.A. Cook, "The complexity of theorem-proving procedures" Proc. 3rd Annual ACM Symp. Theory of Computing , 3 (1971) pp. 151–158 |
| [a5] | R.M. Karp, "Reducibility among combinatorial problems" R.E. Miller (ed.) J.W. Tatcher (ed.) , Complexity of Computer Computations. Proc. Symp. IBM , Plenum (85–103) |
| [a6] | L.A. Levin, "Universal sequential search problems" Problems Inform. Transmission , 9 (1975) pp. 265–266 Probl. Peredach. Inform. , 9 (1973) pp. 115–116 |
| [a7] | M.R. Garey, D.S. Johnson, "Computers and intractability: a guide to the theory of NP-completeness" , Freeman (1979) |
| [a8] | S. French, "Sequencing and scheduling. An introduction to the mathematics of the job-shop" , Horwood (1982) |
| [a9] | E.L. Lawler, J.K. Lenstra, A.H.G. Rinnooy Kan, D.B. Shmoys, "Sequencing and scheduling: algorithms and complexity" , Report NFl , 11.89/03 , Univ. Technology Eindhoven (1989) |
| [a10] | I.M. Anthonisse, K.M. van Hee, J.K. Lenstra, "Resource-constrained project scheduling: an international excercise in  development" Decision Support Systems , 3 (1988) pp. 249–257 development" Decision Support Systems , 3 (1988) pp. 249–257 |
| [a11] | A.S. Belen'kii, E.V. Levner, "Scheduling models and methods in optimal freight transportation planning" Automation and Remote Control , 1 (1989) pp. 1–56 |
| [a12] | M.L. Pindo, L. Schrage, "Stochastic shop scheduling: a survey" M.A.H. Dempster (ed.) J.K. Lenstra (ed.) A.H.G. Rinnooy Kan (ed.) , Deterministic and Stochastic Scheduling , Reidel (1982) pp. 181–196 |
| [a13] | R.H. Möhring, F.J. Radermacher, G. Weiss, "Stochastic scheduling problems I. General strategies" Z. Oper. Res. , 28 (1984) pp. 193–260 |
| [a14] | E.L. Lawler, "Sequencing jobs to minimize total weighted completion time subject to precedence constraints" Ann. Discr. Math. , 2 (1978) pp. 75–90 |
| [a15] | J.K. Lenstra, A.H.G. Rinnooy Kan, P. Brucker, "Complexity of machine scheduling problems" Ann. Discrete Math. , 1 (1977) pp. 343–362 |
| [a16] | E.L. Lawler (ed.) J.K. Lenstra (ed.) A.H.G. Rinnooy Kan (ed.) D.B. Shmoys (ed.) , The traveling salesman problem: a guided tour of combinatorial optimization , Wiley (1985) |
| [a17] | A. Schrijver, "Theory of linear and integer programming" , Wiley (1986) |
| [a18] | G.L. Nemhauser, L.A. Wolsey, "Integer and combinatorial optimization" , Wiley (1988) |
E.V. Levner
Scheduling theory. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Scheduling_theory&oldid=17952