Difference between revisions of "Scattering matrix"
(Importing text file) |
(TeX) |
||
| Line 1: | Line 1: | ||
| − | '' | + | {{TEX|done}} |
| + | ''$S$-matrix'' | ||
An operator (a matrix) describing the process of transfer of a quantum-mechanical system from one state into another under their interaction (scattering). | An operator (a matrix) describing the process of transfer of a quantum-mechanical system from one state into another under their interaction (scattering). | ||
| − | Under scattering, the system moves from one quantum state, the initial one (one may relate it to the time | + | Under scattering, the system moves from one quantum state, the initial one (one may relate it to the time $t=-\infty$), into another, the final one (related to $t=+\infty$). If one denotes the set of quantum numbers describing the initial (final) state by $i$ $(j)$, then the scattering amplitude (the square of whose modulus defines the probability of a given scattering) can be written as $S_{ij}$. The set of all scattering amplitudes forms a table with two inputs, and is called the scattering matrix $S$. |
Determining scattering matrices is a fundamental problem in quantum mechanics and quantum field theory. The scattering matrix contains complete information about the behaviour of a system, provided one knows not only the numerical values, but also the analytical properties of its elements. In particular, its poles determine the bound states of the system (and thus the discrete energy levels). The most important property of a scattering matrix follows from the basic principles of quantum theory: it must be unitary. | Determining scattering matrices is a fundamental problem in quantum mechanics and quantum field theory. The scattering matrix contains complete information about the behaviour of a system, provided one knows not only the numerical values, but also the analytical properties of its elements. In particular, its poles determine the bound states of the system (and thus the discrete energy levels). The most important property of a scattering matrix follows from the basic principles of quantum theory: it must be unitary. | ||
| Line 12: | Line 13: | ||
The notion of an "S-matrix" is applicable in a wider context than only quantum-mechanical systems. | The notion of an "S-matrix" is applicable in a wider context than only quantum-mechanical systems. | ||
| − | The | + | The $S$-matrix was introduced by W. Heisenberg in 1942, [[#References|[a3]]]. It roots go back further, however, to the matrix mechanics, [[#References|[a4]]], of Heisenberg, M. Born and P. Jordan of 1925, and the idea that quantum mechanics should be based (as far as possible) on observable (measurable) quantities. |
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> R.J. Eden, P.V. Landshoff, D.I. Olive, J.C. Polkinghorne, "The analytic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083300/s08330010.png" />-matrix" , Cambridge Univ. Press (1966)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> A.O. Barut, "The theory of the scattering matrix" , Macmillan (1967)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> W. Heisenberg, ''Z. Physik'' , '''120''' (1942–1943) pp. 513; 678</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> A. Messiah, "Quantum mechanics" , '''I''' , North-Holland (1961) pp. Chapt. II</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> D. Iagolnitzer, "The <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083300/s08330011.png" /> matrix" , North-Holland (1978)</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> G.F. Chow, "The analytic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083300/s08330012.png" /> matrix" , Benjamin (1966)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> R.J. Eden, P.V. Landshoff, D.I. Olive, J.C. Polkinghorne, "The analytic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083300/s08330010.png" />-matrix" , Cambridge Univ. Press (1966)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> A.O. Barut, "The theory of the scattering matrix" , Macmillan (1967)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> W. Heisenberg, ''Z. Physik'' , '''120''' (1942–1943) pp. 513; 678</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> A. Messiah, "Quantum mechanics" , '''I''' , North-Holland (1961) pp. Chapt. II</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> D. Iagolnitzer, "The <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083300/s08330011.png" /> matrix" , North-Holland (1978)</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> G.F. Chow, "The analytic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083300/s08330012.png" /> matrix" , Benjamin (1966)</TD></TR></table> | ||
Revision as of 15:06, 17 July 2014
$S$-matrix
An operator (a matrix) describing the process of transfer of a quantum-mechanical system from one state into another under their interaction (scattering).
Under scattering, the system moves from one quantum state, the initial one (one may relate it to the time $t=-\infty$), into another, the final one (related to $t=+\infty$). If one denotes the set of quantum numbers describing the initial (final) state by $i$ $(j)$, then the scattering amplitude (the square of whose modulus defines the probability of a given scattering) can be written as $S_{ij}$. The set of all scattering amplitudes forms a table with two inputs, and is called the scattering matrix $S$.
Determining scattering matrices is a fundamental problem in quantum mechanics and quantum field theory. The scattering matrix contains complete information about the behaviour of a system, provided one knows not only the numerical values, but also the analytical properties of its elements. In particular, its poles determine the bound states of the system (and thus the discrete energy levels). The most important property of a scattering matrix follows from the basic principles of quantum theory: it must be unitary.
Comments
The notion of an "S-matrix" is applicable in a wider context than only quantum-mechanical systems.
The $S$-matrix was introduced by W. Heisenberg in 1942, [a3]. It roots go back further, however, to the matrix mechanics, [a4], of Heisenberg, M. Born and P. Jordan of 1925, and the idea that quantum mechanics should be based (as far as possible) on observable (measurable) quantities.
References
| [a1] | R.J. Eden, P.V. Landshoff, D.I. Olive, J.C. Polkinghorne, "The analytic 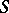 -matrix" , Cambridge Univ. Press (1966) -matrix" , Cambridge Univ. Press (1966) |
| [a2] | A.O. Barut, "The theory of the scattering matrix" , Macmillan (1967) |
| [a3] | W. Heisenberg, Z. Physik , 120 (1942–1943) pp. 513; 678 |
| [a4] | A. Messiah, "Quantum mechanics" , I , North-Holland (1961) pp. Chapt. II |
| [a5] | D. Iagolnitzer, "The 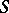 matrix" , North-Holland (1978) matrix" , North-Holland (1978) |
| [a6] | G.F. Chow, "The analytic 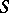 matrix" , Benjamin (1966) matrix" , Benjamin (1966) |
Scattering matrix. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Scattering_matrix&oldid=14456