Scalar
A quantity all values of which can be expressed by one (real) number. More generally, a scalar is an element of some field.
Comments
Generally, the setting is that of a (ground) field 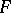 (more generally, a ring
(more generally, a ring 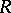 ) and a vector space
) and a vector space 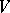 (of functions, vectors, matrices, tensors, etc.) over it (more generally, a module
(of functions, vectors, matrices, tensors, etc.) over it (more generally, a module  ). The elements of
). The elements of 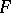 (respectively,
(respectively, 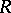 ) are called scalars. If
) are called scalars. If 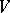 (respectively,
(respectively, 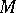 ) is an algebra with unit element
) is an algebra with unit element  , the elements
, the elements  ,
,  in
in 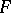 (respectively,
(respectively, 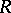 ) are also called scalars. For example, one sometimes speaks of the (
) are also called scalars. For example, one sometimes speaks of the ( )-matrices
)-matrices 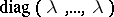 as scalar matrices. The scalar multiples of an element
as scalar matrices. The scalar multiples of an element  (respectively,
(respectively,  ) are the elements
) are the elements  ,
, 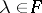 (respectively,
(respectively, 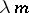 ,
,  ).
).
The term "scalar" comes from the original meaning as a quantity which can be completely specified by one (real) number.
A scalar field on a manifold  is a function on
is a function on  ; that is, a scalar field, or field of scalars, is a tensor field (cf. Tensor bundle) of rank
; that is, a scalar field, or field of scalars, is a tensor field (cf. Tensor bundle) of rank  . These are the scalars in the algebra of tensor fields on
. These are the scalars in the algebra of tensor fields on 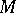 over the ring of functions on
over the ring of functions on  .
.
A scalar operator on, say, a complex Banach space is a scalar multiple of the identity operator.
Given a left module  over a ring
over a ring 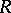 and an
and an 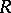 -algebra
-algebra 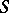 , one forms the tensor product
, one forms the tensor product  . This is a module over
. This is a module over 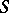 . The module
. The module  is said to be obtained from
is said to be obtained from  by extension of scalars.
by extension of scalars.
References
| [a1] | P.M. Cohn, "Algebra" , 1 , Wiley (1982) pp. 70 |
| [a2] | K. Rektorys (ed.) , Applicable mathematics , Iliffe (1969) pp. 270; 290 |
Scalar. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Scalar&oldid=13931