Sample variance
sample dispersion
A scalar characteristic of the disperson, or spread, of a sample (consisting of real numbers) relative to a fixed point  (called the centre of dispersion). It is numerically equal to the sum of the squares of the deviations of the values from
(called the centre of dispersion). It is numerically equal to the sum of the squares of the deviations of the values from  . For real-valued random variables
. For real-valued random variables  , the variable
, the variable
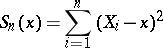 |
is the sample variance about  . The variables
. The variables  are often assumed to be independent and identically distributed in discussions about
are often assumed to be independent and identically distributed in discussions about  . Since, for any
. Since, for any  ,
,
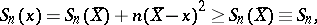 |
where 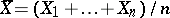 , the sample variance about
, the sample variance about  will be minimal when
will be minimal when 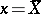 . A small value of
. A small value of 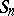 indicates a concentration of the sample elements about
indicates a concentration of the sample elements about  and, conversely, a large value of
and, conversely, a large value of 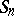 indicates a large scattering of the sample elements. The concept of a sample variance extends to that of a sample covariance matrix for multivariate samples.
indicates a large scattering of the sample elements. The concept of a sample variance extends to that of a sample covariance matrix for multivariate samples.
References
| [1] | S.S. Wilks, "Mathematical statistics" , Wiley (1962) |
Sample variance. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Sample_variance&oldid=18175