Saddle
A type of arrangement of the trajectories of an autonomous system of planar ordinary differential equations
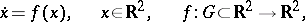 | (*) |
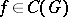 , where
, where 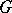 is the domain of uniqueness, in a neighbourhood of a singular point (equilibrium position)
is the domain of uniqueness, in a neighbourhood of a singular point (equilibrium position) 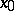 . This type is characterized as follows. There is a neighbourhood
. This type is characterized as follows. There is a neighbourhood 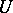 of
of 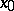 such that for all trajectories of the system that start in
such that for all trajectories of the system that start in 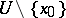 , both the positive and negative semi-trajectories are diverging (as time passes they leave any compact set
, both the positive and negative semi-trajectories are diverging (as time passes they leave any compact set 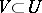 ). The exceptions are four trajectories, called the separatrices of the saddle. For two of these, the negative semi-trajectories are diverging and the positive semi-trajectories converge to
). The exceptions are four trajectories, called the separatrices of the saddle. For two of these, the negative semi-trajectories are diverging and the positive semi-trajectories converge to 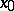 , and for the other two the situation is just the opposite. The first two separatrices are called stable, and the second two, unstable. The stable separatrices, completed by
, and for the other two the situation is just the opposite. The first two separatrices are called stable, and the second two, unstable. The stable separatrices, completed by 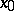 , form a smooth curve through
, form a smooth curve through 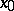 — the stable manifold of the saddle. The unstable separatrices, together with
— the stable manifold of the saddle. The unstable separatrices, together with 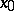 , form the smooth unstable manifold of the saddle. The point
, form the smooth unstable manifold of the saddle. The point 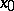 is also called the saddle.
is also called the saddle.
The saddle  is unstable in the sense of Lyapunov (cf. Lyapunov stability). Its Poincaré index is
is unstable in the sense of Lyapunov (cf. Lyapunov stability). Its Poincaré index is 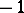 (cf. Singular point). For a system (*) of class
(cf. Singular point). For a system (*) of class 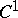 (
(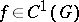 ) with a non-zero matrix
) with a non-zero matrix 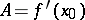 , a stationary point
, a stationary point 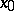 is a saddle when the eigenvalues
is a saddle when the eigenvalues 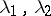 of
of 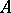 satisfy the condition
satisfy the condition 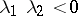 (a simple saddle; see Fig. a, where
(a simple saddle; see Fig. a, where  ) but it can also be a saddle when
) but it can also be a saddle when 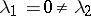 , or
, or 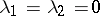 .
.

Figure: s083020a
In any of these cases the separatrices of the saddle are tangential at 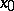 to the directions defined by the eigenvectors of
to the directions defined by the eigenvectors of 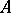 .
.
If the system (*) is linear (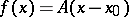 , where
, where 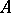 is a constant matrix with eigenvalues
is a constant matrix with eigenvalues 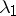 and
and 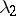 ), then a point
), then a point 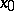 of it is a saddle only when
of it is a saddle only when 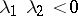 . In this case the separatrices of the saddle
. In this case the separatrices of the saddle 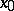 are rectilinear, and all the other trajectories (distinct from
are rectilinear, and all the other trajectories (distinct from 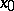 ) are affine images of the hyperbolas of the form
) are affine images of the hyperbolas of the form 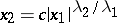 ,
, 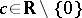 (Fig. b).
(Fig. b).

Figure: s083020b
The term "saddle" is also used for any of the arrangements of the trajectories of the system (*) in a neighbourhood 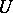 of an isolated stationary point
of an isolated stationary point 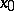 , where only a finite number
, where only a finite number 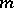 (
(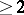 ) of trajectories in
) of trajectories in 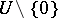 approaches
approaches 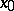 and where each of them, completed by
and where each of them, completed by 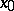 , touches at this point in a definite direction (an
, touches at this point in a definite direction (an 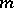 -separatrix saddle). Certain types of stationary points of autonomous systems of ordinary differential equations of order
-separatrix saddle). Certain types of stationary points of autonomous systems of ordinary differential equations of order 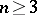 are also called saddles. For references, see Singular point of a differential equation.
are also called saddles. For references, see Singular point of a differential equation.
Comments
Cf. also Hyperbolic point and Hyperbolic set and the references given there.
Saddle. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Saddle&oldid=15481