S-duality
stationary duality, Spanier duality
A duality in homotopy theory which exists (in the absence of restrictions imposed on the dimensions of spaces) for the analogues of ordinary homotopy and cohomotopy groups in the suspension category — for the $ S $- homotopy and $ S $- cohomotopy groups or stationary homotopy and cohomotopy groups, forming extra-ordinary (generalized) homology and cohomology theories. A suspension category, or $ S $- category, is a category whose objects are topological spaces $ X $, while its morphisms are classes $ \{ f \} $ of $ S $- homotopic mappings $ f $ from a $ p $- fold suspension $ S ^ { p } X _ { 1 } $ into $ S ^ { p } X _ { 2 } $, $ f $ and $ g: S ^ { q } X _ { 1 } \rightarrow S ^ { q } X _ { 2 } $ being considered as $ S $- homotopic if there exists an $ r \geq \max { ( p, q) } $ such that the suspensions $ S ^ { {r-p} } f $ and $ S ^ { {r-q} } g $ are homotopic in the ordinary sense. The set $ \{ X _ { 1 } , X _ { 2 } \} $ of such classes, which are known as $ S $- mappings, constitutes an Abelian group with respect to the so-called track addition [1], [2], [4], [5]. The group $ \{ X _ { 1 } , X _ { 2 } \} $ is the limit of the direct spectrum of the sets $ [ S ^ { k } X _ { 1 } , S ^ { k } X _ { 2 } ] $ of ordinary homotopy classes with suspension mappings as projections; if $ k $ is sufficiently large, it is a group spectrum with homomorphisms. There exists an isomorphism $ S: \{ X _ { 1 } , X _ { 2 } \} \rightarrow \{ SX _ { 1 } , SX _ { 2 } \} $ in which the corresponding elements are represented by one and the same mapping $ S ^ { p } X _ { 1 } \rightarrow S ^ { p } X _ { 2 } $, $ p \geq 1 $. The $ n $- dual polyhedron of the polyhedron $ X $ in a sphere $ S ^ { n } $ is an arbitrary polyhedron $ D _ { n } X $ in $ S ^ { n } $ which is an $ S $- deformation retract of the complement $ S ^ { n } \setminus X $, i.e. the morphism corresponding to the imbedding $ D _ { n } X \subset S ^ { n } \setminus X $ is an $ S $- equivalence. The polyhedron $ D _ { n } X $ exists for all $ X $, and $ X $ may be considered as $ D _ { n } ^ { 2 } X $.
For any polyhedra $ X _ { 1 } , X _ { 2 } $ and any polyhedra $ D _ { n } X _ { 1 } $ and $ D _ { n } X _ { 2 } $ which are dual to them, there exists a unique mapping
$$ D _ { n } : \{ X _ { 1 } , X _ { 2 } \} \rightarrow \ \{ D _ { n } X _ { 2 } , D _ { n } X _ { 1 } \} $$
satisfying the following conditions:
a) It is an involutory contravariant functorial isomorphism, i.e. $ D _ { n } $ is a homomorphism such that if
$$ i : X _ { 1 } \subset X _ { 2 } \ \textrm{ and } \ i ^ \prime : D _ { n } X _ { 2 } \subset D _ { n } X _ { 1 } , $$
then
$$ D _ { n } \{ i \} = \{ i ^ \prime \} ; $$
if
$$ \{ f _ { 1 } \} \in \{ X _ { 1 } , X _ { 2 } \} \ \textrm{ and } \ \ \{ f _ { 2 } \} \in \{ X _ { 2 } , X _ { 3 } \} , $$
then
$$ D _ { n } { ( \{ f _ { 2 } \} \cdot \{ f _ { 1 } \} ) } = \ D _ { n } \{ f _ { 1 } \} \cdot D _ { n } \{ f _ { 2 } \} ; $$
if $ \theta $ is an element of $ \{ X _ { 1 } , X _ { 2 } \} $ or of $ \{ D _ { n } X _ { 2 } , D _ { n } X _ { 1 } \} $, then $ D _ { n } D _ { n } \theta = \theta $.
b) The following relations are valid:
$$ SD _ { n } = D _ { {n+1} } \ \textrm{ and } \ D _ { {n+1} } S = D _ { n } , $$
where $ SD _ { n } X _ { i } $ and $ D _ { n } X _ { i } $ are considered as polyhedra, $ { ( {n+1} ) } $- dual to polyhedra $ X _ { i } $ and, correspondingly, $ SX _ { i } $, $ i = 1, 2; $ this means that it does not depend on $ n $ and is stationary with respect to suspension.
c) It satisfies the equation
$$ D _ { a } ^ { n } \theta _ { * } = { ( D _ { n } \theta ) } ^ { * } D _ { a } ^ { n } , $$
where
$$ \theta _ { * } : H _ { p } { ( X _ { 1 } ) } \rightarrow H _ { p } { ( X _ { 2 } ) } $$
and
$$ { ( D _ { n } \theta ) } ^ { * } : H ^ { { {n-p} -1} } { ( D _ { n } X _ { 1 } ) } \rightarrow H ^ { { {n-p} -1} } { ( D _ { n } X _ { 2 } ) } $$
are homomorphisms of the above homology and cohomology groups, induced by $ S $- mappings $ \theta \in \{ X _ { 1 } , X _ { 2 } \} $ and $ D _ { n } \theta $, and
$$ D _ { a } : H _ { p } { ( X _ { i } ) } \rightarrow H ^ { { {n-p} -1} } { ( D _ { n } X _ { i } ) } ,\ {i=1} , 2 , $$
is an isomorphism obtained from the isomorphism of Alexander duality by replacing the set $ S ^ { n } \setminus X _ { i } $ by its $ S $- deformation retract $ D _ { n } X _ { i } $.
The construction of $ D _ { n } $ is based on the representation of a given mapping as the composition of an imbedding and an $ S $- deformation retract.
The $ S $- homotopy group $ \Sigma _ { p } { ( X) } $ of a space $ X $ is the group $ \{ S ^ { p } , X \} $, and the $ S $- cohomotopy group $ \Sigma ^ { p } { ( X) } $ of $ X $ is the group $ \{ X, S ^ { p } \} $. As in ordinary homotopy theory, one defines the homomorphisms
$$ \phi _ { p } : \Sigma _ { p } { ( X) } \rightarrow H _ { p } { ( X) } , $$
$$ \phi ^ { p } : \Sigma ^ { p } { ( X) } \rightarrow H ^ { p } { ( X) } . $$
Regarding the spheres $ S ^ { p } $ and $ S ^ { { {n-p} -1} } $ as $ n $- dual leads to the isomorphisms
$$ D _ { n } : \Sigma _ { p } { ( X) } \rightarrow \Sigma ^ { { {n-p} -1} } { ( D _ { n } X) } $$
and to the commutative diagram
$$ \begin{array}{ccc} {\Sigma _ { p } { ( X) } } & \stackrel{ \phi _ p }{\rightarrow} &{H _ { p } { ( X) } } \\ { { {D _ { n } } } \downarrow } &{} &{\downarrow { {D _ { a } ^ { n } } } } \\ {\Sigma ^ { { {n-p} -1} } { ( D _ { n } ^ { X } ) } } & \stackrel{\phi ^{n-p-1}}{\rightarrow} &{H ^ { { {n-p} -1} } { ( D _ { n } X) } } \\ \end{array} $$
Thus, the isomorphism $ D _ { n } $ connects $ S $- homotopy and $ S $- cohomotopy groups, just as the isomorphism of Alexander duality $ D _ { a } ^ { n } $ connects the homology and cohomology groups. Any duality in the $ S $- category entails a duality of ordinary homotopy classes if the conditions imposed on the space entail the existence of a one-to-one correspondence between the set of the above classes and the set of $ S $- homotopy classes.
Examples of dual assumptions in this theory include Hurewicz's isomorphism theorem and Hopf's classification theorem. $ D _ { n } $ converts one of these theorems into the other, which means that $ S $- homotopy groups are replaced by $ S $- cohomotopy groups, homology groups by cohomology groups, the mapping $ \phi _ { p } $ by the mapping $ \phi ^ { { {n-p} -1} } $, the smallest dimension with a non-trivial homology group by the largest dimension with a non-trivial cohomology group, and vice versa. In ordinary homotopy theory the definition of an $ n $- cohomotopy group requires that the dimension of the space does not exceed $ {2n-2} $( or, more generally, that the space be $ { { ( 2n-1) }} $- coconnected, $ n > 1 $), which impairs the perfectly general nature of duality.
There are several trends of generalization of the theory: e.g. studies are made of spaces with the $ S $- homotopy type of polyhedra, the relative case, a theory with supports, etc. [3], [5], , [7]. The theory was one of the starting points in the development of stationary homotopy theory [8].
References
| [1] | E.H. Spanier, "Duality and 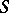 -theory" Bull. Amer. Math. Soc. , 62 (1956) pp. 194–203 MR0085506 -theory" Bull. Amer. Math. Soc. , 62 (1956) pp. 194–203 MR0085506 |
| [2] | E.H. Spanier, J.H.C. Whitehead, "Duality in homotopy theory" Mathematika , 2 : 3 (1955) pp. 56–80 MR0074823 Zbl 0064.17202 |
| [3] | E.H. Spanier, J.H.C. Whitehead, "Duality in relative homotopy theory" Ann. of Math. , 67 : 2 (1958) pp. 203–238 MR0105105 Zbl 0092.15701 |
| [4] | M.G. Barratt, "Track groups 1; 2" Proc. London Math. Soc. , 5 (1955) pp. 71–106; 285–329 |
| [5] | E.H. Spanier, J.H.C. Whitehead, "The theory of carriers and 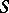 -theory" , Algebraic geometry and Topology (A Symp. in honor of S. Lefschetz) , Princeton Univ. Press (1957) pp. 330–360 MR0084772 -theory" , Algebraic geometry and Topology (A Symp. in honor of S. Lefschetz) , Princeton Univ. Press (1957) pp. 330–360 MR0084772 |
| [6a] | B. Eckmann, P.J. Hilton, "Groupes d'homotopie et dualité. Groupes absolus" C.R. Acad. Sci. Paris , 246 : 17 (1958) pp. 2444–2447 MR0100261 Zbl 0092.39901 |
| [6b] | B. Eckmann, P.J. Hilton, "Groupes d'homotopie et dualité. Suites exactes" C.R. Acad. Sci. Paris , 246 : 18 (1958) pp. 2555–2558 MR0100262 Zbl 0092.40001 |
| [6c] | B. Eckmann, P.J. Hilton, "Groupes d'homotopie et dualité. Coefficients" C.R. Acad. Sci. Paris , 246 : 21 (1958) pp. 2991–2993 MR0100263 Zbl 0092.40101 |
| [6d] | B. Eckmann, P.J. Hilton, "Transgression homotopique et cohomologique" C.R. Acad. Sci. Paris , 247 : 6 (1958) pp. 620–623 MR0100264 Zbl 0092.40102 |
| [6e] | B. Eckmann, P.J. Hilton, "Décomposition homologique d'un polyhèdre simplement connexe" C.R. Acad. Sci. Paris , 248 : 14 (1959) pp. 2054–2056 |
| [7] | E.H. Spanier, "Algebraic topology" , McGraw-Hill (1966) MR0210112 MR1325242 Zbl 0145.43303 |
| [8] | G.W. Whitehead, "Recent advances in homotopy theory" , Amer. Math. Soc. (1970) MR0309097 Zbl 0217.48601 |
S-duality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=S-duality&oldid=49677