Runge theorem
A theorem on the possibility of polynomially approximating holomorphic functions, first proved by C. Runge (1885) (cf. also Approximation of functions of a complex variable).
Let 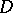 be a simply-connected domain in the complex
be a simply-connected domain in the complex  -plane. Then any function
-plane. Then any function 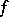 holomorphic in
holomorphic in 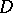 can be approximated uniformly on compact sets inside
can be approximated uniformly on compact sets inside 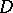 by polynomials in
by polynomials in  . More precisely, for any compact set
. More precisely, for any compact set 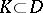 and
and 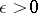 there is a polynomial
there is a polynomial 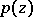 with complex coefficients such that
with complex coefficients such that 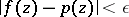 for all
for all 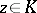 .
.
In other words: Any function 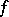 holomorphic in a simply-connected domain
holomorphic in a simply-connected domain 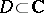 can be represented as a series of polynomials in
can be represented as a series of polynomials in  converging absolutely and uniformly to
converging absolutely and uniformly to 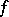 on compact sets inside
on compact sets inside 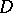 .
.
An equivalent statement of Runge's theorem: Let  be a compact set in
be a compact set in 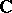 with connected complement
with connected complement 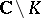 ; then any function holomorphic in a neighbourhood of
; then any function holomorphic in a neighbourhood of 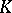 can be approximated uniformly on
can be approximated uniformly on 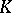 by polynomials in
by polynomials in  . In this formulation, Runge's theorem is a special case of Mergelyan's theorem (cf. Mergelyan theorem).
. In this formulation, Runge's theorem is a special case of Mergelyan's theorem (cf. Mergelyan theorem).
The following theorem on rational approximation is also called Runge's theorem: Any function 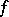 holomorphic in a domain
holomorphic in a domain 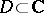 can be uniformly approximated on compact sets inside
can be uniformly approximated on compact sets inside 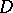 by rational functions with poles outside
by rational functions with poles outside  .
.
Runge's theorem has many applications in the theory of functions of a complex variable and in functional analysis. A theorem analogous to Runge's theorem is valid for non-compact Riemann surfaces. An extension of Runge's theorem to functions of several complex variables is the Oka–Weil theorem (see Oka theorems).
References
| [1] | A.I. Markushevich, "A short course on the theory of analytic functions" , Moscow (1978) (In Russian) |
| [2] | B.V. Shabat, "Introduction of complex analysis" , 1 , Moscow (1976) (In Russian) |
Comments
For more about Runge's theorem and its generalizations, such as Walsh' theorem, the Keldysh theorem, the Lavrent'ev theorem, see [a6], [a1], Chapt. VIII, and [a3], Chapt. III, for the case of the complex plane; [a2], Sect. 25, for the case of Riemann surfaces; and [a4], Sect. 7, for the case of several complex variables.
References
| [a1] | R.B. Burchel, "An introduction to classical complex analysis" , 1 , Acad. Press (1979) |
| [a2] | O. Forster, "Lectures on Riemann surfaces" , Springer (1981) (Translated from German) |
| [a3] | D. Gaier, "Lectures on complex approximation" , Birkhäuser (1987) (Translated from German) |
| [a4] | J. Wermer, "Banach algebras and several complex variables" , Springer (1976) pp. Chapt. 13 |
| [a5] | W. Rudin, "Real and complex analysis" , McGraw-Hill (1978) pp. 24 |
| [a6] | A.I. Markushevich, "Theory of functions of a complex variable" , 3 , Chelsea (1977) pp. Sect. 3.12 (Translated from Russian) |
Runge theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Runge_theorem&oldid=13069