Routh theorem
A theorem that enables one to determine, using a Routh scheme, the number of complex roots with positive real part of a polynomial 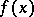 with real coefficients (in the regular case).
with real coefficients (in the regular case).
Write 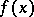 in the form
in the form
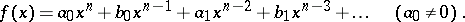 |
The Routh scheme of this polynomial is defined to be the array of numbers
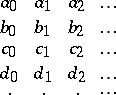 |
In this scheme, the first two rows consist of the coefficients of 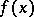 , and every row from the third onwards is obtained from the previous two as follows: subtract from the first line that multiple of the second which makes the first entry equal to zero. By deleting this first zero, one obtains the described row. For example, in the third row,
, and every row from the third onwards is obtained from the previous two as follows: subtract from the first line that multiple of the second which makes the first entry equal to zero. By deleting this first zero, one obtains the described row. For example, in the third row,
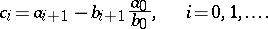 |
The number of entries in the first row of the Routh scheme is equal to the integer part of 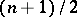 , in the second, to that of
, in the second, to that of 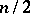 , and in the
, and in the 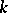 -th (for
-th (for 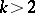 ), the number of entries is one less than in the
), the number of entries is one less than in the 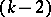 -nd. The whole scheme contains
-nd. The whole scheme contains 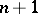 rows. The case when the entries in the first column are all different from zero is called regular.
rows. The case when the entries in the first column are all different from zero is called regular.
Routh's theorem: For a polynomial with real coefficients in the regular case, the number of roots lying in the right half-plane (that is, having positive real part) is equal to the number of changes of sign in the sequence of entries in the first column of the Routh scheme. In the regular case, the polynomial cannot have roots lying on the imaginary axis. Routh's criterion: Every root of a polynomial 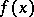 with real coefficients has negative real part if and only if the entries in the first column of the Routh scheme are all non-zero and have the same sign. These theorems were established by E.J. Routh [1]. Routh's scheme can also be used to determine the number of roots of a polynomial in the right half-plane in certain non-regular cases.
with real coefficients has negative real part if and only if the entries in the first column of the Routh scheme are all non-zero and have the same sign. These theorems were established by E.J. Routh [1]. Routh's scheme can also be used to determine the number of roots of a polynomial in the right half-plane in certain non-regular cases.
The construction of a Routh scheme is possible only for polynomials with given numerical coefficients. There is a more widely used method, in which the role of the Routh scheme is played by the Hurwitz matrix, and that of the first column by the sequence of principal minors 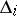 ,
, 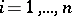 (see Routh–Hurwitz criterion; Minor). Then the analogue of Routh's theorem is the Routh–Hurwitz theorem: If the minors
(see Routh–Hurwitz criterion; Minor). Then the analogue of Routh's theorem is the Routh–Hurwitz theorem: If the minors 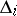 are all non-zero, then the number of roots of
are all non-zero, then the number of roots of 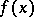 lying in the right half-plane is equal to the number of changes of sign in the sequence
lying in the right half-plane is equal to the number of changes of sign in the sequence
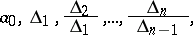 |
and 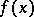 has no roots lying on the imaginary axis. Under certain extra conditions, this method can be used in case some of the minors
has no roots lying on the imaginary axis. Under certain extra conditions, this method can be used in case some of the minors 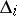 are equal to zero.
are equal to zero.
References
| [1] | E.J. Routh, "A treatise on the stability of a given state of motion" , Macmillan (1877) |
| [2] | E.J. Routh, "The advanced part of a treatise on the dynamics of a system of rigid bodies" , Macmillan (1905) |
| [3] | A.M. Lyapunov, "Stability of motion" , Acad. Press (1966) (Translated from Russian) |
| [4] | F.R. [F.R. Gantmakher] Gantmacher, "The theory of matrices" , 1 , Chelsea, reprint (1977) (Translated from Russian) |
Comments
References
| [a1] | N. [N. Obreshchkov] Obreschkoff, "Verteilung und Berechnung der Nulllstellen reeller Polynome" , Deutsch. Verlag Wissenschaft. (1963) (Translated from Russian) |
Routh theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Routh_theorem&oldid=17043