Routh-Hurwitz criterion
Hurwitz criterion
A necessary and sufficient condition for all the roots of a polynomial
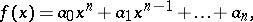 |
with real coefficients and 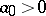 , to have negative real parts. It consists of the following: All principal minors
, to have negative real parts. It consists of the following: All principal minors 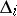 ,
, 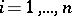 , of the Hurwitz matrix
, of the Hurwitz matrix 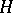 are positive (cf. Minor). Here
are positive (cf. Minor). Here 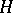 is the matrix of order
is the matrix of order  whose
whose 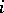 -th row has the form
-th row has the form
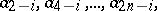 |
where, by definition, 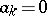 if
if 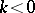 or
or 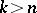 (the Hurwitz condition or the Routh–Hurwitz condition). This criterion was obtained by A. Hurwitz [1] and is a generalization of the work of E.J. Routh (see Routh theorem).
(the Hurwitz condition or the Routh–Hurwitz condition). This criterion was obtained by A. Hurwitz [1] and is a generalization of the work of E.J. Routh (see Routh theorem).
A polynomial 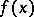 satisfying the Hurwitz condition is called a Hurwitz polynomial, or, in applications of the Routh–Hurwitz criterion in the stability theory of oscillating systems, a stable polynomial. There are other criteria for the stability of polynomials, such as the Routh criterion, the Liénard–Chipart criterion, and methods for determining the number of real roots of a polynomial are also known.
satisfying the Hurwitz condition is called a Hurwitz polynomial, or, in applications of the Routh–Hurwitz criterion in the stability theory of oscillating systems, a stable polynomial. There are other criteria for the stability of polynomials, such as the Routh criterion, the Liénard–Chipart criterion, and methods for determining the number of real roots of a polynomial are also known.
References
| [1] | A. Hurwitz, "Ueber die Bedingungen, unter welchen eine Gleichung nur Wurzeln mit negativen reellen Theilen besitzt" Math. Ann. , 46 (1895) pp. 273–284 |
| [2] | F.R. [F.R. Gantmakher] Gantmacher, "The theory of matrices" , 1 , Chelsea, reprint (1977) (Translated from Russian) |
Comments
See also Routh theorem.
Routh-Hurwitz criterion. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Routh-Hurwitz_criterion&oldid=33371