Rotations diagram

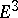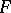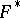A surface in the elliptic space defined by isometric smooth surfaces and in the Euclidean space 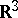in the same way as the rotation indicatrix is defined for infinitesimal deformations in 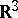. L. Bianchi was the first to mention surfaces in elliptic space coincident with the rotations diagram, in examining the spherical representation of a deformation base for surfaces, where he showed that it coincides with the representation in the sense of Clifford for the asymptotic lines in the rotations diagram.

Let 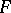and 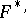be isometric smooth identically-oriented surfaces. At the points 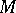and 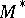corresponding in isometry, the trihedra formed by the tangent vectors 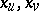and to the corresponding isometric pairs of curves 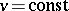and 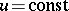and the normals and 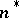are equal, i.e.

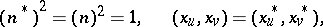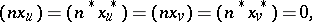and therefore one of them is obtained from another by rotation around an axis with direction unit vector 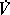through an angle 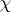(defined up to 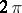). Let

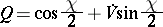be the quaternion, equal in modulus to 1 and defined up to its sign, representing this rotation. The set of such quaternions parametrized by the points 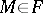(or 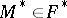) defines a set of points in the elliptic space, which is called the rotations diagram for the isometric surfaces 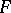and 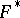. For example, if 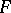and 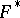are isometric pieces of cylinders, then the rotations diagram is a part of a Clifford surface, and a minimal Clifford surface corresponds to circular cylinders. If , there is an elliptic plane outside the rotations diagram, and under a geodesic mapping of the elliptic space into the Euclidean space,

the image of the rotations diagram is the rotation indicatrix for some infinitesimal deformation of the median surface corresponding to 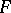and 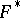(see Cohn-Vossen transformation) (it is regular if ).

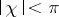The properties of the rotations diagrams for isometric surfaces of positive Gaussian curvature are analogous to those of rotation indicatrices; for example, the specific internal curvature of the rotations diagram is always negative, and therefore it plays the same part as the rotation indicatrix when examining the isometry of convex surfaces.

References

[a1]	M. Spivak, "A comprehensive introduction to differential geometry" , 1979 , Publish or Perish pp. 1–5
[a2]	A.V. Pogorelov, "Intrinsic geometry of surfaces" , Amer. Math. Soc. (1973) (Translated from Russian)
[a3]	A.V. Pogorelov, "Extrinsic geometry of convex surfaces" , Amer. Math. Soc. (1973) (Translated from Russian)