Rotation surface
surface of rotation, rotational surface
A surface generated by the rotation of a plane curve 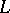 around an axis in its plane. If
around an axis in its plane. If 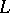 is defined by the equations
is defined by the equations 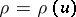 ,
, 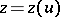 , the position vector of the surface of rotation is
, the position vector of the surface of rotation is 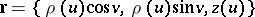 , where
, where  is the parameter of the curve
is the parameter of the curve 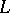 ,
, 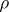 is the distance between a point on the surface and the axis
is the distance between a point on the surface and the axis  of rotation and
of rotation and  is the angle of rotation. The line element of the surface of rotation is
is the angle of rotation. The line element of the surface of rotation is
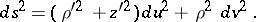 |
The Gaussian curvature is 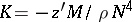 , the mean curvature is
, the mean curvature is 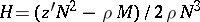 , where
, where 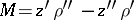 ,
, 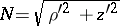 . The lines
. The lines 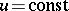 are called parallels of the surface of rotation and are circles located in a plane normal to the axis of rotation, with their centres on this axis. The lines
are called parallels of the surface of rotation and are circles located in a plane normal to the axis of rotation, with their centres on this axis. The lines 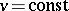 are called meridians; they are all congruent to the rotating curve and lie in planes passing through the axis of rotation. The meridians and the parallels of a surface of rotation are its curvature lines and form an isothermal net.
are called meridians; they are all congruent to the rotating curve and lie in planes passing through the axis of rotation. The meridians and the parallels of a surface of rotation are its curvature lines and form an isothermal net.
A surface of rotation allows for a deformation into another surface of rotation, under which its net of curvature lines is preserved and therefore is a principal base of the deformation. The umbilical points (cf. Umbilical point) of a surface of rotation are characterized by the property that the centre of curvature of the meridian lies on the axis of rotation. The product of the radius of a parallel by the cosine of the angle of intersection of the surface of rotation with the parallel is constant along a geodesic (Clairaut's theorem).
The only minimal surface of rotation is the catenoid. A ruled surface of rotation is a one-sheet hyperboloid or one of its degeneracies: a cylinder, a cone or a plane. A surface of rotation with more than one axis of rotation is a sphere or a plane.
The metric of a surface of rotation can be presented in the form
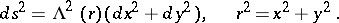 | (1) |
For the existence of metrics of the form (1) and for isometric immersions of these in 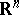 as surfaces of rotation see [1].
as surfaces of rotation see [1].
References
| [1] | I.Kh. Sabitov, , Abstracts Coll. Diff. Geom. (August 1989, Eger, Hungary) pp. 47–48 |
Comments
References
| [a1] | M. Berger, B. Gostiaux, "Differential geometry: manifolds, curves, and surfaces" , Springer (1988) (Translated from French) |
| [a2] | M.P. Do Carmo, "Differential geometry of curves and surfaces" , Prentice-Hall (1976) pp. 145 |
| [a3] | M. Spivak, "A comprehensive introduction to differential geometry" , 1979 , Publish or Perish pp. 1–5 |
| [a4] | K. Leichtweiss, "Einführung in die Differentialgeometrie" , Springer (1973) |
Rotation surface. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Rotation_surface&oldid=18444