Rotation of a vector field
on a plane
One of the characteristics of a vector field that are invariant under homotopy. Let  be a vector field on a domain
be a vector field on a domain  of the Euclidean plane
of the Euclidean plane  and let
and let  be the angle between
be the angle between  and some fixed direction; the rotation of
and some fixed direction; the rotation of  will then be the increment of the angle
will then be the increment of the angle  when going around a closed oriented curve
when going around a closed oriented curve  along which
along which  , divided by
, divided by  . For instance, if
. For instance, if 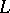 is a smooth curve of class
is a smooth curve of class 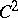 , the rotation of the field
, the rotation of the field  (or
(or  ) tangent to
) tangent to 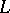 (or normal to
(or normal to 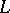 ) along
) along  is equal to the total curvature of
is equal to the total curvature of 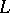 divided by
divided by  ; if
; if 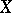 is a vector field (with or without isolated singular points) on a domain
is a vector field (with or without isolated singular points) on a domain 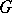 , with Jordan boundary
, with Jordan boundary  , then the rotation of
, then the rotation of 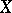 on
on 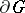 is equal to the sum of the indices of the singular points of
is equal to the sum of the indices of the singular points of 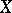 in the closure of
in the closure of 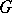 (cf. Singular point, index of a). The rotation of a vector field remains unchanged during a homotopic deformation of
(cf. Singular point, index of a). The rotation of a vector field remains unchanged during a homotopic deformation of 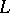 which does not pass through the singular points of
which does not pass through the singular points of 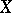 .
.
A generalization consists of the concept of the index of a vector field  on an
on an  -dimensional manifold
-dimensional manifold 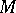 , at an isolated point
, at an isolated point 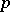 of
of  . It is defined as the degree of
. It is defined as the degree of 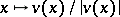 , as a mapping from a small sphere around
, as a mapping from a small sphere around 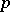 to the unit sphere (cf. Degree of a mapping). It is related to the Euler characteristic. See also Poincaré theorem; Kronecker formula.
to the unit sphere (cf. Degree of a mapping). It is related to the Euler characteristic. See also Poincaré theorem; Kronecker formula.
Comments
Cf. also Rotation number of a curve, which is the rotation of the unit tangent vector field of the curve along that curve.
References
| [a1] | M. Berger, B. Gostiaux, "Differential geometry: manifolds, curves, and surfaces" , Springer (1988) (Translated from French) |
| [a2] | W. Greub, S. Halperin, R. Vanstone, "Connections, curvature, and cohomology" , 1–3 , Acad. Press (1972) |
| [a3] | A. Pollack, "Differential topology" , Prentice-Hall (1974) |
Rotation of a vector field. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Rotation_of_a_vector_field&oldid=16123