Difference between revisions of "Rotation number"
(Importing text file) |
m |
||
| Line 1: | Line 1: | ||
| + | {{DEF}} | ||
| + | |||
Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082650/r0826501.png" /> be a regular curve, i.e. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082650/r0826502.png" /> is smooth and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082650/r0826503.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082650/r0826504.png" />. Then there is a continuous piecewise-differentiable function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082650/r0826505.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082650/r0826506.png" />, the normalized velocity vector at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082650/r0826507.png" />, is equal to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082650/r0826508.png" />. Moreover, the difference <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082650/r0826509.png" /> is independent of the choice of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082650/r08265010.png" />. | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082650/r0826501.png" /> be a regular curve, i.e. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082650/r0826502.png" /> is smooth and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082650/r0826503.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082650/r0826504.png" />. Then there is a continuous piecewise-differentiable function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082650/r0826505.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082650/r0826506.png" />, the normalized velocity vector at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082650/r0826507.png" />, is equal to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082650/r0826508.png" />. Moreover, the difference <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082650/r0826509.png" /> is independent of the choice of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082650/r08265010.png" />. | ||
Revision as of 15:07, 6 May 2012
This page is deficient and requires revision. Please see Talk:Rotation number for further comments.
Let 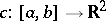 be a regular curve, i.e.
be a regular curve, i.e.  is smooth and
is smooth and 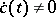 for all
for all 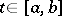 . Then there is a continuous piecewise-differentiable function
. Then there is a continuous piecewise-differentiable function 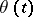 such that
such that  , the normalized velocity vector at
, the normalized velocity vector at 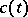 , is equal to
, is equal to 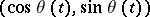 . Moreover, the difference
. Moreover, the difference  is independent of the choice of
is independent of the choice of 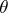 .
.

Figure: r082650a
Now, let 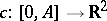 be a piecewise-smooth regular closed curve and let
be a piecewise-smooth regular closed curve and let 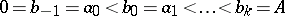 partition
partition 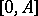 into intervals such that
into intervals such that  restricted to
restricted to 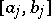 is differentiable for all
is differentiable for all 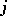 . Let
. Let 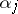 be the exterior angle between the tangent vectors at the corner at
be the exterior angle between the tangent vectors at the corner at 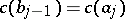 , i.e.
, i.e.  is the angle between
is the angle between 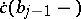 and
and 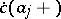 (with
(with 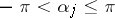 ). The number
). The number
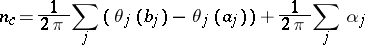 |
is called the rotation number of the curve  .
.
If 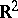 is identified with the complex plane
is identified with the complex plane 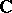 and
and  is smooth (so that all
is smooth (so that all 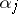 are zero), then
are zero), then 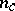 is the winding number of the closed curve
is the winding number of the closed curve 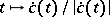 with respect to the origin.
with respect to the origin.
Let 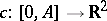 be piecewise-smooth, regular, closed, and simple (i.e. no self-intersections), and suppose that the exterior angles are always
be piecewise-smooth, regular, closed, and simple (i.e. no self-intersections), and suppose that the exterior angles are always 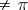 in absolute value. Then the so-called Umlaufsatz says that
in absolute value. Then the so-called Umlaufsatz says that 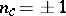 , depending on the orientation. From this it is easy to calculate the
, depending on the orientation. From this it is easy to calculate the 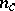 of closed curves with self-intersections. For instance, the rotation number of the figure eight curve is zero.
of closed curves with self-intersections. For instance, the rotation number of the figure eight curve is zero.
It readily follows from these results that, e.g., the sum of the interior angles of a convex  -gon is
-gon is 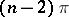 . There also result the various formulas for triangles (and other figures) made up of circle segments, such as
. There also result the various formulas for triangles (and other figures) made up of circle segments, such as 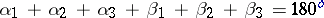 in the case of the circle segment triangle depicted on the left in Fig.a2; and
in the case of the circle segment triangle depicted on the left in Fig.a2; and 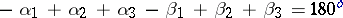 for the circle segment triangle depicted on the right in Fig.a2. Here the
for the circle segment triangle depicted on the right in Fig.a2. Here the  denote the number of degrees of the circle segments in question,
denote the number of degrees of the circle segments in question, 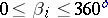 ,
, 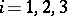 .
.

Figure: r082650b
For more on the planar geometry of circle segment triangles and such, see, e.g., [a2], [a3].
References
| [a1] | W. Klingenberg, "A course in differential geometry" , Springer (1978) pp. §2.1 (Translated from German) |
| [a2] | L. Bieberbach, "Zur Euklidischen Geometrie der Kreisbogendreiecke" Math. Ann. , 130 (1955) pp. 46–86 |
| [a3] | W.K.B. Holz, "Das ebene obere Dreieck. Eine Aufgabestellung" , Selbstverlag Hagen (1944) |
| [a4] | H. Hopf, "Über die Drehung der Tangenten und Sehen ebener Kurven" Compositio Math. , 2 (1935) pp. 50–62 |
Rotation number. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Rotation_number&oldid=12710