Root vector

of a linear transformation 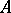of a vector space over a field

A vector in the kernel of the linear transformation , where 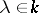and is a positive integer depending on 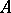and . The number 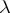is necessarily an eigenvalue of . If, under these conditions, , one says that is a root vector of height belonging to .

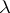The concept of a root vector generalizes the concept of an eigenvector of a transformation 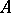: The eigenvectors are precisely the root vectors of height 1. The set of root vectors belonging to a fixed eigenvalue 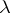is a linear subspace of which is invariant under . It is known as the root subspace belonging to the eigenvalue . Root vectors belonging to different eigenvalues are linearly independent; in particular, 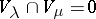if .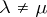

Let 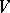be finite-dimensional. If all roots of the characteristic polynomial of 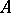are in 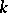(e.g. if 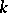is algebraically closed), then 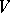decomposes into the direct sum of different root spaces:

(*)

This decomposition is a special case of the weight decomposition of a vector space relative to a splitting nilpotent Lie algebra of linear transformations: The Lie algebra in this case is the one-dimensional subalgebra generated by 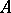in the Lie algebra of all linear transformations of (see Weight of a representation of a Lie algebra).

If the matrix of relative to some basis is a Jordan matrix, then the components of the decomposition (*) may be described as follows: The root subspace 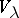is the linear hull of the set of basis vectors which correspond to Jordan cells with eigenvalue .

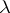References

[1]	V.V. Voevodin, "Algèbre linéare" , MIR (1976) (Translated from Russian)
[2]	A.I. Mal'tsev, "Foundations of linear algebra" , Freeman (1963) (Translated from Russian)