Root
An  -th root of a number
-th root of a number  is a number
is a number 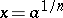 whose
whose  -th power
-th power 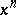 is equal to
is equal to  .
.
A root of an algebraic equation over a field 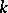 ,
,
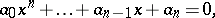 |
is an element  belonging to
belonging to 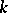 or to an extension of
or to an extension of  (cf. Extension of a field) such that when
(cf. Extension of a field) such that when  is substituted for
is substituted for  the equation becomes an identity. A root of this equation is also called a root or zero of the polynomial
the equation becomes an identity. A root of this equation is also called a root or zero of the polynomial
 |
If  is a root of a polynomial
is a root of a polynomial 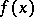 , then
, then 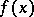 is divisible (without remainder) by
is divisible (without remainder) by  (see Bezout theorem). Every polynomial
(see Bezout theorem). Every polynomial 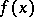 with real or complex coefficients has at least one root (hence as many roots as its degree, counting multiplicities). The polynomial
with real or complex coefficients has at least one root (hence as many roots as its degree, counting multiplicities). The polynomial 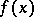 may be expressed as a product
may be expressed as a product
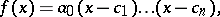 |
where  are its roots. If some of the roots
are its roots. If some of the roots  of
of 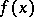 are equal, their common value is called a multiple root (if a root occurs
are equal, their common value is called a multiple root (if a root occurs 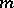 times,
times, 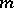 is called the multiplicity of that root).
is called the multiplicity of that root).
A root of unity is an element of a field 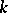 satisfying the equation
satisfying the equation 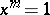 for some natural number
for some natural number 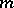 . The roots of unity form a subgroup of the multiplicative group of
. The roots of unity form a subgroup of the multiplicative group of 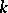 . Conversely, all elements of any finite subgroup of the multiplicative group of a field
. Conversely, all elements of any finite subgroup of the multiplicative group of a field 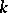 are roots of unity (cf. Fermat little theorem) and the subgroup itself is cyclic. This is true, in particular, for the subgroup
are roots of unity (cf. Fermat little theorem) and the subgroup itself is cyclic. This is true, in particular, for the subgroup 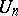 of all roots of unity of a given degree
of all roots of unity of a given degree  contained in the algebraic closure
contained in the algebraic closure 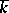 of
of 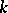 , i.e. the subgroup of all
, i.e. the subgroup of all 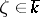 satisfying the equation
satisfying the equation 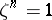 . If
. If  is relatively prime to the characteristic of
is relatively prime to the characteristic of 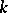 (or if the characteristic is 0), then the group
(or if the characteristic is 0), then the group 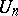 is of order
is of order  and its generators are known as primitive
and its generators are known as primitive  -th roots of unity. The number of such roots in
-th roots of unity. The number of such roots in  is given by the Euler function
is given by the Euler function 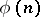 , i.e. the number of residues
, i.e. the number of residues 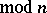 which are relatively prime to
which are relatively prime to  . In a field of characteristic
. In a field of characteristic 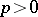 there are no
there are no  -th roots of unity other than 1.
-th roots of unity other than 1.
If the field 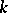 is finitely generated over its prime subfield, then the number of roots of unity in
is finitely generated over its prime subfield, then the number of roots of unity in 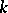 is finite.
is finite.
In the field of complex numbers, a number  is an
is an  -th root of unity if and only if
-th root of unity if and only if  and
and 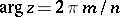 , where
, where 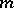 and
and  are integers, i.e. if and only if
are integers, i.e. if and only if
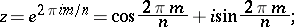 |
in this case the primitive roots of unity are exactly those for which 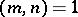 . In the complex plane, the
. In the complex plane, the  -th roots of unity coincide with the vertices of the regular
-th roots of unity coincide with the vertices of the regular  -gon inscribed in the unit circle; this explains the connection of roots of unity with the problem of squaring the circle (construction of polygons, cf. Geometric constructions).
-gon inscribed in the unit circle; this explains the connection of roots of unity with the problem of squaring the circle (construction of polygons, cf. Geometric constructions).
Roots of unity appear in number theory as the values of various important number-theoretical functions (Abelian numerical characters; Legendre symbol; Möbius function; norm-residue symbol; etc.). In field theory and algebraic number theory an important position is occupied by fields obtained by adjunction of roots of unity to some ground field (see Cyclotomic field; Cyclotomic extension; Kummer extension).
References
| [1] | B.L. van der Waerden, "Algebra" , 1–2 , Springer (1967–1971) (Translated from German) |
| [2] | S. Lang, "Algebra" , Addison-Wesley (1984) |
Comments
For the concept of a root in Lie algebra theory see Lie algebra, semi-simple and Root system.
Root. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Root&oldid=17528