Robin problem
equilibrium problem, electrostatic problem
A problem on the distribution of a positive Borel measure  on the boundary
on the boundary 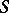 of a compact set
of a compact set 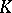 in the
in the  -dimensional Euclidean space
-dimensional Euclidean space 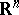 ,
, 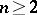 , which generates a constant Newton potential for
, which generates a constant Newton potential for 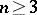 , or constant logarithmic potential for
, or constant logarithmic potential for 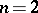 , on any connected component of the interior of
, on any connected component of the interior of 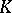 , i.e. the problem on the equilibrium distribution of an electric charge
, i.e. the problem on the equilibrium distribution of an electric charge  on the surface
on the surface 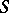 of a conductor
of a conductor  .
.
In the simplest classical case when 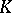 is a closed domain in
is a closed domain in 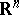 homeomorphic to the sphere, bounded by a smooth simple surface or (when
homeomorphic to the sphere, bounded by a smooth simple surface or (when 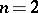 ) by a curve
) by a curve 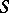 of class
of class 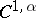 ,
, 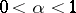 ,
, 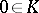 , the solution of Robin's problem is reduced to finding a non-trivial solution
, the solution of Robin's problem is reduced to finding a non-trivial solution  ,
, 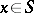 , of the homogeneous Fredholm-type integral equation of the second kind
, of the homogeneous Fredholm-type integral equation of the second kind
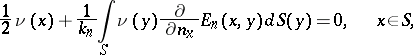 | (1) |
under the normalization condition
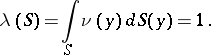 | (2) |
Here
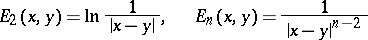 |
for  ,
,  is the distance between two points
is the distance between two points 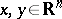 ,
, 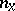 is the direction of the exterior normal to
is the direction of the exterior normal to 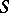 at the point
at the point 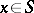 ,
, 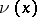 is the derivative, or density, of the absolutely-continuous measure
is the derivative, or density, of the absolutely-continuous measure 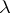 with respect to the Lebesgue measure on
with respect to the Lebesgue measure on 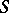 ,
,
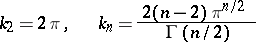 |
for 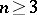 , and
, and 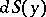 is the area element of the surface
is the area element of the surface 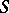 . Equation (1) is obtained when one considers the interior Neumann problem for the domain bounded by
. Equation (1) is obtained when one considers the interior Neumann problem for the domain bounded by 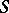 under vanishing boundary conditions, since the simple-layer potential
under vanishing boundary conditions, since the simple-layer potential
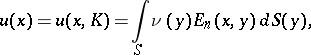 |
called the Robin potential, equilibrium potential or capacity potential, should, according to the condition of Robin's problem, have a constant value on 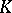 (see Potential theory, and also [2]). The solution
(see Potential theory, and also [2]). The solution 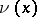 for the problem (1), (2) under the indicated conditions always exists in the class of continuous functions
for the problem (1), (2) under the indicated conditions always exists in the class of continuous functions 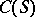 . The measure
. The measure
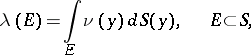 |
which provides a solution of the Robin problem, is called the equilibrium measure. In a more complicated case, when the boundary of the compact set  consists of a finite number of non-intersecting simple closed surfaces or (when
consists of a finite number of non-intersecting simple closed surfaces or (when 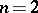 ) curves of class
) curves of class 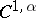 ,
, 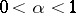 (see [2]), the Robin problem is solved in a similar way. Moreover, on bounded connected components of the open set
(see [2]), the Robin problem is solved in a similar way. Moreover, on bounded connected components of the open set 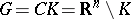 the Robin potential
the Robin potential 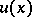 also preserves its constant value, i.e. on the boundaries of these components the density
also preserves its constant value, i.e. on the boundaries of these components the density 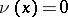 .
.
Let the compact set 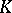 be connected. The constant value of the Robin potential
be connected. The constant value of the Robin potential 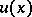 on
on 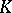 ,
,
 |
is called the Robin constant of the compact set 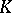 . For
. For 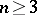 it is related to the harmonic, or Newton, capacity
it is related to the harmonic, or Newton, capacity 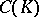 of
of 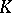 by the simple relation
by the simple relation 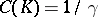 ; moreover,
; moreover, 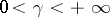 ,
, 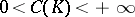 . For
. For 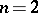 , the Robin constant can assume all values
, the Robin constant can assume all values  ; the harmonic capacity is then expressed by the formula
; the harmonic capacity is then expressed by the formula 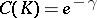 .
.
In another way, the equilibrium measure 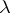 is defined as the measure which yields the minimum of the energy integral
is defined as the measure which yields the minimum of the energy integral
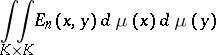 |
in the class of all measures 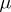 concentrated on
concentrated on 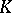 and such that
and such that 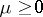 ,
, 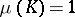 . Such a measure
. Such a measure 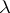 in the case of a compact set
in the case of a compact set 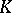 with a smooth boundary coincides with the one found above, but it exists also in the general case of an arbitrary compact set
with a smooth boundary coincides with the one found above, but it exists also in the general case of an arbitrary compact set 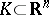 ,
, 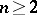 , if only
, if only  . The corresponding equilibrium potential
. The corresponding equilibrium potential
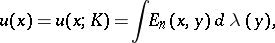 |
which is a generalization of the Robin potential, preserves the constant value 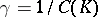 for
for 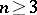 , or
, or 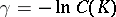 for
for 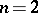 , everywhere on
, everywhere on 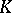 except perhaps at the points of some set of capacity zero.
except perhaps at the points of some set of capacity zero.
The name "Robin problem" is connected with studies of G. Robin (see [1]).
References
| [1] | G. Robin, "Sur la distribution de l'électricité à la surface des conducteurs fermés et des conducteurs ouverts" Ann. Sci. Ecole Norm. Sup. , 3 (1886) pp. 31–358 |
| [2] | N.M. Günter, "Potential theory and its applications to basic problems of mathematical physics" , F. Ungar (1967) (Translated from Russian) |
| [3] | N.S. Landkof, "Foundations of modern potential theory" , Springer (1972) (Translated from Russian) |
| [4] | W.K. Hayman, P.B. Kennedy, "Subharmonic functions" , 1 , Acad. Press (1976) |
Comments
In [1] Robin reconsiders and generalizes a problem formulated by S. Poisson (1811).
References
| [a1] | M. Tsuji, "Potential theory in modern function theory" , Chelsea, reprint (1975) |
Robin problem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Robin_problem&oldid=14200