Robin constant
A numerical characteristic of a set of points in a Euclidean space 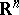 ,
, 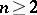 , closely connected with the capacity of the set.
, closely connected with the capacity of the set.
Let 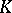 be a compact set in
be a compact set in  , and let
, and let 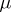 be a positive Borel measure concentrated on
be a positive Borel measure concentrated on 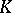 and normalized by the condition
and normalized by the condition 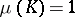 . The integral
. The integral
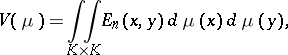 |
where
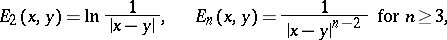 |
and 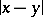 is the distance between two points
is the distance between two points 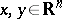 , is the energy of
, is the energy of 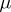 (cf. Energy of measures). The Robin constant of the compact set
(cf. Energy of measures). The Robin constant of the compact set 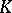 is the lower bound
is the lower bound 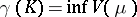 over all measures
over all measures 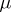 of the indicate type. If
of the indicate type. If 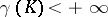 , then this bound is finite and is attained for some (unique) equilibrium, or capacitary, measure
, then this bound is finite and is attained for some (unique) equilibrium, or capacitary, measure 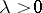 ,
, 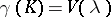 ,
, 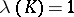 , concentrated on
, concentrated on 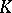 ; if
; if 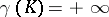 , then
, then 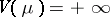 for all measures
for all measures 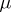 of the indicated type. The Robin constant of
of the indicated type. The Robin constant of 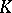 is related to its capacity by the formula
is related to its capacity by the formula
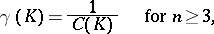 |
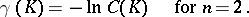 |
If the boundary 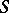 of
of 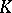 is sufficiently smooth, for example, if it consists of a finite number of pairwise non-intersecting simple closed surfaces (for
is sufficiently smooth, for example, if it consists of a finite number of pairwise non-intersecting simple closed surfaces (for 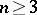 ) or curves (for
) or curves (for 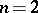 ) of class
) of class  ,
, 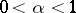 , then the equilibrium measure
, then the equilibrium measure 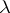 is concentrated on the part
is concentrated on the part 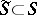 which forms the boundary of that connected component of the complement
which forms the boundary of that connected component of the complement 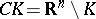 which contains the point at infinity. The equilibrium potential, Robin potential or capacity potential, i.e. the potential of the equilibrium measure
which contains the point at infinity. The equilibrium potential, Robin potential or capacity potential, i.e. the potential of the equilibrium measure
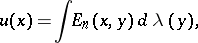 |
in this case assumes a constant value on 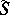 , equal to
, equal to 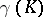 , which allows one to calculate the Robin constant of a compact set in the simplest cases (see Robin problem). For instance, the Robin constant of a disc of radius
, which allows one to calculate the Robin constant of a compact set in the simplest cases (see Robin problem). For instance, the Robin constant of a disc of radius 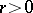 in
in 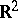 is
is 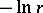 , and the Robin constant of a ball of radius
, and the Robin constant of a ball of radius 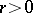 in
in 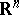 ,
, 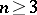 , is
, is  . In the case of an arbitrary compact set
. In the case of an arbitrary compact set 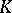 of positive capacity,
of positive capacity,  everywhere and
everywhere and 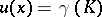 everywhere on the support
everywhere on the support 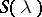 of the equilibrium measure
of the equilibrium measure 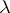 , except possibly at the points of some polar set; moreover,
, except possibly at the points of some polar set; moreover,  .
.
Let 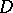 be a domain in the extended complex plane
be a domain in the extended complex plane 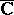 containing inside it the point at infinity and having a Green function
containing inside it the point at infinity and having a Green function 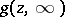 with pole at infinity. Then the following representation holds:
with pole at infinity. Then the following representation holds:
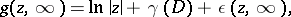 | (1) |
where 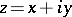 is a complex variable,
is a complex variable, 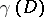 is the Robin constant of the domain
is the Robin constant of the domain 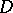 and
and 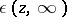 is a harmonic function in
is a harmonic function in 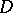 ; moreover,
; moreover,
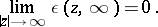 |
The Robin constant of the domain 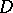 , defined by (1), coincides with the Robin constant of the compact set
, defined by (1), coincides with the Robin constant of the compact set 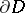 :
: 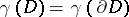 . If the Green function for the domain
. If the Green function for the domain 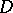 does not exist, then one assumes that
does not exist, then one assumes that 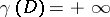 .
.
By generalizing the representation (1) to a Riemann surface 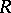 which has a Green function, one can obtain a local representation of the Green function
which has a Green function, one can obtain a local representation of the Green function  with pole
with pole 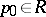 :
:
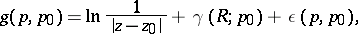 | (2) |
where 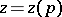 is a local uniformizing parameter in a neighbourhood of the pole
is a local uniformizing parameter in a neighbourhood of the pole  ,
, 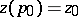 ,
, 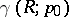 is the Robin constant of the Riemann surface
is the Robin constant of the Riemann surface 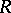 relative to the pole
relative to the pole 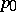 , and
, and 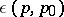 is a harmonic function in a neighbourhood of
is a harmonic function in a neighbourhood of 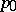 ; moreover,
; moreover, 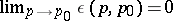 . For Riemann surfaces
. For Riemann surfaces 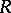 which do not have a Green function one assumes
which do not have a Green function one assumes 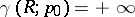 . In expression (2) the value of the Robin constant
. In expression (2) the value of the Robin constant 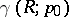 depends now on the choice of the pole
depends now on the choice of the pole 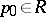 . However, the relations
. However, the relations 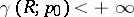 and
and 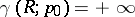 are independent of the choice of the pole. This allows one to use the notion of a Robin constant in the classification of Riemann surfaces (cf. Riemann surfaces, classification of).
are independent of the choice of the pole. This allows one to use the notion of a Robin constant in the classification of Riemann surfaces (cf. Riemann surfaces, classification of).
References
| [1] | R. Nevanilinna, "Analytic functions" , Springer (1970) (Translated from German) |
| [2] | S. [S. Stoilov] Stoilow, "Leçons sur les principes topologiques de la théorie des fonctions analytiques" , Gauthier-Villars (1938) |
| [3] | L. Sario, M. Nakai, "Classification theory of Riemann surfaces" , Springer (1970) |
Comments
See also the references quoted in Capacity; Energy of measures; Robin problem.
Robin constant. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Robin_constant&oldid=18330