Ring of sets
From Encyclopedia of Mathematics
A collection 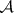 of subsets of a set
of subsets of a set 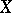 satisfying:
satisfying:
i) 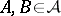 implies
implies 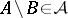 ;
;
ii) 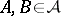 implies
implies 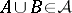 .
.
It follows that 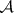 is also closed under finite intersections, since
is also closed under finite intersections, since 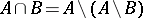 . If
. If 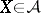 , the ring of sets is an algebra of sets.
, the ring of sets is an algebra of sets.
A 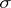 -ring of sets is a ring of sets satisfying additionally
-ring of sets is a ring of sets satisfying additionally
a) 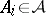 ,
, 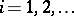 , implies
, implies 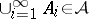 .
.
A 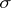 -ring is closed under countable intersections. If
-ring is closed under countable intersections. If 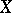 is a member of a
is a member of a 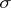 -ring
-ring 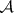 of subsets of
of subsets of 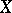 , then
, then 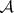 is a
is a  -algebra (cf. Additive class of sets; Algebra of sets).
-algebra (cf. Additive class of sets; Algebra of sets).
References
| [a1] | H.R. Pitt, "Integration, measure and probability" , Oliver&Boyd (1963) pp. 2–3 |
How to Cite This Entry:
Ring of sets. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Ring_of_sets&oldid=14767
Ring of sets. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Ring_of_sets&oldid=14767
This article was adapted from an original article by M. Hazewinkel (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article