Right-ordered group
A group on whose set of elements a total order  (cf. Totally ordered group) is defined such that for all
(cf. Totally ordered group) is defined such that for all  the inequality
the inequality  implies
implies  . The set
. The set  of positive elements of
of positive elements of  is a pure (i.e.
is a pure (i.e.  ) linear (i.e.
) linear (i.e.  ) sub-semi-group. Every pure linear sub-semi-group
) sub-semi-group. Every pure linear sub-semi-group  of an arbitrary group defines a right order, namely
of an arbitrary group defines a right order, namely  if and only if
if and only if  .
.
The group  of automorphisms of a totally-ordered set
of automorphisms of a totally-ordered set 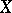 can be right ordered in a natural manner. Every right-ordered group is order-isomorphic to some subgroup of
can be right ordered in a natural manner. Every right-ordered group is order-isomorphic to some subgroup of  for a suitable totally-ordered set (cf. [1]). An Archimedean right-ordered group, i.e. a right-ordered group for which Archimedes' axiom holds (cf. Archimedean group), is order-isomorphic to a subgroup of the additive group of real numbers. In contrast with (two-sided) ordered groups, there are non-commutative right-ordered groups without proper convex subgroups (cf. Convex subgroup). The class of right-ordered groups is closed under lexicographic extension. The system of all convex subgroups of a right-ordered group
for a suitable totally-ordered set (cf. [1]). An Archimedean right-ordered group, i.e. a right-ordered group for which Archimedes' axiom holds (cf. Archimedean group), is order-isomorphic to a subgroup of the additive group of real numbers. In contrast with (two-sided) ordered groups, there are non-commutative right-ordered groups without proper convex subgroups (cf. Convex subgroup). The class of right-ordered groups is closed under lexicographic extension. The system of all convex subgroups of a right-ordered group  is totally ordered with respect to inclusion and is complete. This system is solvable (cf. also Solvable group) if and only if for any positive elements
is totally ordered with respect to inclusion and is complete. This system is solvable (cf. also Solvable group) if and only if for any positive elements  there is a natural number
there is a natural number  such that
such that  . If the group has a solvable subgroup system
. If the group has a solvable subgroup system  whose factors are torsion-free, then
whose factors are torsion-free, then  can be right-ordered in such a way that all subgroups in
can be right-ordered in such a way that all subgroups in  become convex. In a locally nilpotent right-ordered group the system of convex subgroups is solvable.
become convex. In a locally nilpotent right-ordered group the system of convex subgroups is solvable.
A group  can be right-ordered if and only if for any finite system
can be right-ordered if and only if for any finite system
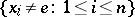 |
of elements of  there are numbers
there are numbers 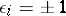 ,
,  , such that the semi-group generated by the set
, such that the semi-group generated by the set  does not contain the identity element of
does not contain the identity element of  .
.
Every lattice ordering of a group 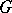 is the intersection of some of its right-orderings (cf. Lattice-ordered group).
is the intersection of some of its right-orderings (cf. Lattice-ordered group).
References
| [1] | A.I. Kokorin, V.M. Kopytov, "Fully ordered groups" , Israel Program Sci. Transl. (1974) (Translated from Russian) |
| [2] | R.B. Mura, A. Rhemtulla, "Orderable groups" , M. Dekker (1977) |
Comments
A group  that admits a total order such that with this order
that admits a total order such that with this order 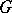 becomes a right-ordered group, is called right-orderable. Such an order on
becomes a right-ordered group, is called right-orderable. Such an order on  is called a right order or right ordering.
is called a right order or right ordering.
Some more concepts and results concerning right-ordered groups can be found in [a1]–[a4].
References
| [a1] | M. Anderson, T. Feil, "Lattice-ordered groups. An introduction" , Reidel (1988) pp. 35; 38ff |
| [a2] | A.M.W. Glass (ed.) W.Ch. Holland (ed.) , Lattice-ordered groups. Advances and techniques , Kluwer (1989) |
| [a3] | W.B. Powell, "Universal aspects of the theory of lattice-ordered groups" J. Martinez (ed.) , Ordered Algebraic Structures , Kluwer (1989) pp. 11–50 |
| [a4] | M.R. Darnell, "Recent results on the free lattice ordered group over a right-orderable group" J. Martinez (ed.) , Ordered Algebraic Structures , Kluwer (1989) pp. 51–57 |
Right-ordered group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Right-ordered_group&oldid=15087