Riesz theorem(2)
Riesz's theorem on the representation of a subharmonic function: If  is a subharmonic function in a domain
is a subharmonic function in a domain 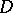 of a Euclidean space
of a Euclidean space  ,
, 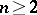 , then there exists a unique positive Borel measure
, then there exists a unique positive Borel measure 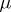 on
on 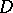 such that for any relatively compact set
such that for any relatively compact set 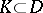 the Riesz representation of
the Riesz representation of  as the sum of a potential and a harmonic function
as the sum of a potential and a harmonic function 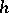 is valid:
is valid:
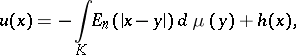 | (1) |
where
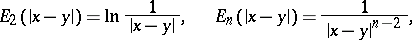 |
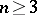 and
and 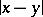 is the distance between the points
is the distance between the points 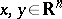 (see ). The measure
(see ). The measure 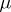 is called the associated measure for the function
is called the associated measure for the function  or the Riesz measure.
or the Riesz measure.
If 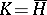 is the closure of a domain
is the closure of a domain 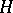 and if, moreover, there exists a generalized Green function
and if, moreover, there exists a generalized Green function  , then formula (1) can be written in the form
, then formula (1) can be written in the form
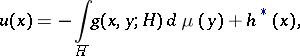 | (2) |
where 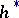 is the least harmonic majorant of
is the least harmonic majorant of  in
in 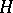 .
.
Formulas (1) and (2) can be extended under certain additional conditions to the entire domain 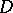 (see Subharmonic function, and also , ).
(see Subharmonic function, and also , ).
Riesz's theorem on the mean value of a subharmonic function: If  is a subharmonic function in a spherical shell
is a subharmonic function in a spherical shell 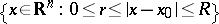 , then its mean value
, then its mean value 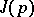 over the area of the sphere
over the area of the sphere 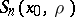 with centre at
with centre at 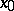 and radius
and radius 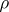 ,
, 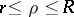 , that is,
, that is,
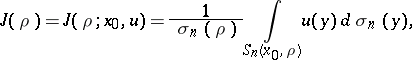 |
where 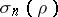 is the area of
is the area of 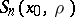 , is a convex function with respect to
, is a convex function with respect to 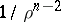 for
for 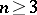 and with respect to
and with respect to 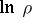 for
for 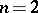 . If
. If  is a subharmonic function in the entire ball
is a subharmonic function in the entire ball 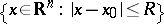 , then
, then 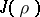 is, furthermore, a non-decreasing continuous function with respect to
is, furthermore, a non-decreasing continuous function with respect to 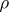 under the condition that
under the condition that 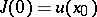 (see ).
(see ).
Riesz's theorem on analytic functions of Hardy classes 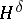 ,
, 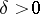 : If
: If 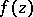 is a regular analytic function in the unit disc
is a regular analytic function in the unit disc 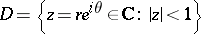 of Hardy class
of Hardy class 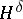 ,
, 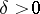 (see Boundary properties of analytic functions; Hardy classes), then the following relations hold:
(see Boundary properties of analytic functions; Hardy classes), then the following relations hold:
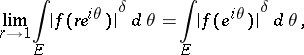 |
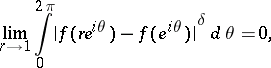 |
where 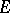 is an arbitrary set of positive measure on the circle
is an arbitrary set of positive measure on the circle 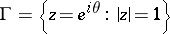 , and
, and 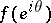 are the boundary values of
are the boundary values of 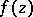 on
on 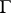 . Moreover,
. Moreover, 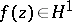 if and only if its integral is continuous in the closed disc
if and only if its integral is continuous in the closed disc 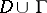 and is absolutely continuous on
and is absolutely continuous on 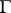 (see [2]).
(see [2]).
Theorems 1)–3) were proved by F. Riesz (see , [2]).
References
| [1a] | F. Riesz, "Sur les fonctions sous harmoniques et leur rapport à la theorie du potentiel I" Acta Math. , 48 (1926) pp. 329–343 |
| [1b] | F. Riesz, "Sur les fonctions sous harmoniques et leur rapport à la theorie du potentiel II" Acta Math. , 54 (1930) pp. 321–360 |
| [2] | F. Riesz, "Ueber die Randwerte einer analytischer Funktion" Math. Z. , 18 (1923) pp. 87–95 |
| [3] | I.I. Privalov, "Subharmonic functions" , Moscow-Leningrad (1937) (In Russian) |
| [4] | I.I. [I.I. Privalov] Priwalow, "Randeigenschaften analytischer Funktionen" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian) |
| [5] | W.K. Hayman, P.B. Kennedy, "Subharmonic functions" , 1 , Acad. Press (1976) |
Comments
In abstract potential theory, a potential on an open set 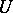 is a superharmonic function
is a superharmonic function 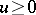 on
on 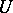 such that any harmonic minorant of
such that any harmonic minorant of  is negative on
is negative on 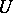 . The Riesz representation theorem now takes the form: Any superharmonic function on
. The Riesz representation theorem now takes the form: Any superharmonic function on 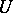 can be written uniquely as the sum of a potential and a harmonic function on
can be written uniquely as the sum of a potential and a harmonic function on 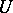 , see [a2].
, see [a2].
In an ordered Banach space 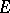 , the Riesz interpolation property means that, for any
, the Riesz interpolation property means that, for any 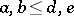 , there exists a
, there exists a 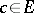 such that
such that 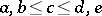 . An equivalent form is the decomposition property: for
. An equivalent form is the decomposition property: for 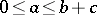 there exist
there exist 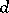 and
and  such that
such that 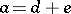 and
and 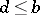 ,
, 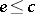 . These properties are used in the theory of Choquet simplexes (cf. Choquet simplex) and in the fine theory of hyperharmonic functions, see [a1] and [a2].
. These properties are used in the theory of Choquet simplexes (cf. Choquet simplex) and in the fine theory of hyperharmonic functions, see [a1] and [a2].
References
| [a1] | L. Asimow, A.J. Ellis, "Convexity theory and its applications in functional analysis" , Acad. Press (1980) |
| [a2] | C. Constantinescu, A. Cornea, "Potential theory on harmonic spaces" , Springer (1972) |
Riesz theorem(2). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Riesz_theorem(2)&oldid=12058