Riesz system
A concept in the theory of orthogonal systems (cf. Orthonormal system). Let a complete system of functions  be fixed in the space
be fixed in the space  . It is considered normalized, or, more generally, almost normalized, i.e. there are numbers
. It is considered normalized, or, more generally, almost normalized, i.e. there are numbers  and
and  for which
for which  for all
for all  . Weakening the requirement concerning the orthogonality of the system
. Weakening the requirement concerning the orthogonality of the system  one assumes that there exists a complete system of functions
one assumes that there exists a complete system of functions  in
in  such that
such that  ,
, 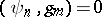 for all
for all 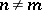 . In particular, when the system
. In particular, when the system 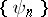 is orthonormal,
is orthonormal,  for all
for all 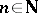 . If a series
. If a series
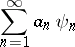 |
converges to a function 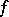 in
in 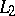 , then
, then 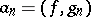 for all
for all  . Thus it makes sense to call the number
. Thus it makes sense to call the number  the
the  -th Fourier coefficient of the function
-th Fourier coefficient of the function 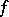 with respect to the system
with respect to the system 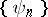 . In the proofs of a number of theorems in the theory of orthogonal series, the Bessel inequality and the Riesz–Fischer theorem are of great importance. In the general case these theorems are not valid, therefore one has to single out the special class of Riesz systems, i.e. systems
. In the proofs of a number of theorems in the theory of orthogonal series, the Bessel inequality and the Riesz–Fischer theorem are of great importance. In the general case these theorems are not valid, therefore one has to single out the special class of Riesz systems, i.e. systems  satisfying
satisfying
1) for any function 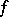 the series of the squares of the Fourier coefficients is absolutely convergent, i.e.
the series of the squares of the Fourier coefficients is absolutely convergent, i.e.
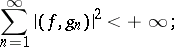 |
2) for any sequence of numbers 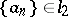 there exists a function
there exists a function  for which the
for which the  are its Fourier coefficients with respect to the system
are its Fourier coefficients with respect to the system 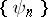 , that is,
, that is, 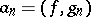 for all
for all 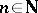 .
.
The first requirement on the system  replaces the Bessel inequality, the second the Riesz–Fischer theorem. N.K. Bari has proved (see [2]) that a system
replaces the Bessel inequality, the second the Riesz–Fischer theorem. N.K. Bari has proved (see [2]) that a system 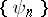 is a Riesz system if and only if there exists a continuous linear operator
is a Riesz system if and only if there exists a continuous linear operator 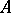 , invertible in
, invertible in 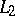 , such that the system of functions
, such that the system of functions  is complete and orthonormal. Therefore, a Riesz system is also called a Riesz basis, equivalent to an orthonormal basis. Bari has indicated a convenient criterion for being a Riesz system. A complete system of functions
is complete and orthonormal. Therefore, a Riesz system is also called a Riesz basis, equivalent to an orthonormal basis. Bari has indicated a convenient criterion for being a Riesz system. A complete system of functions 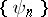 in
in 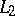 is a Riesz system if and only if the Gram matrix
is a Riesz system if and only if the Gram matrix  determines a continuous invertible linear operator in
determines a continuous invertible linear operator in  . Under an arbitrary permutation of the elements of a Riesz system one obtains again a Riesz system. Conversely, if a basis in
. Under an arbitrary permutation of the elements of a Riesz system one obtains again a Riesz system. Conversely, if a basis in  is still a basis after any permutation of its elements, then by normalizing it one obtains a Riesz system. A natural generalization of a Riesz system is obtained by replacing
is still a basis after any permutation of its elements, then by normalizing it one obtains a Riesz system. A natural generalization of a Riesz system is obtained by replacing 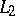 by the closure of the linear span of a system
by the closure of the linear span of a system 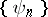 with respect to the norm of the Hilbert space from which the elements
with respect to the norm of the Hilbert space from which the elements 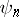 are taken (see [4]).
are taken (see [4]).
References
| [1] | N.K. Bari, "Sur les bases dans l'espace de Hilbert" Dokl. Akad. Nauk SSSR , 54 (1946) pp. 379–382 |
| [2] | N.K. Bari, "Biorthogonal systems and bases in Hilbert space" Uchen. Zap. Moskov. Gos. Univ. , 148 : 4 (1951) pp. 69–107 (In Russian) |
| [3] | I.C. [I.Ts. Gokhberg] Gohberg, M.G. Krein, "Introduction to the theory of linear nonselfadjoint operators" , Transl. Math. Monogr. , 18 , Amer. Math. Soc. (1969) (Translated from Russian) |
| [4] | V.F. Gaposhkin, "Lacunary series and independent functions" Russian Math. Surveys , 21 : 6 (1966) pp. 1–82 Uspekhi Mat. Nauk , 21 : 6 (1966) pp. 3–82 |
Riesz system. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Riesz_system&oldid=16931