Riesz potential
 -potential
-potential
A potential of the form
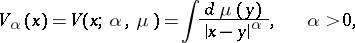 |
where  is a positive Borel measure of compact support on the Euclidean space
is a positive Borel measure of compact support on the Euclidean space  ,
,  , and
, and  is the distance between the points
is the distance between the points  . When
. When  and
and  , the Riesz potential coincides with the classical Newton potential; when
, the Riesz potential coincides with the classical Newton potential; when  and
and  , the limit case of the Riesz potential is in some sense the logarithmic potential. When
, the limit case of the Riesz potential is in some sense the logarithmic potential. When 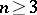 and
and  , the Riesz potential is a superharmonic function on the entire space
, the Riesz potential is a superharmonic function on the entire space  ; moreover, in the classical case
; moreover, in the classical case  , outside the support
, outside the support  of
of  , the potential
, the potential  is a harmonic function. When
is a harmonic function. When  , the Riesz potential
, the Riesz potential  is a subharmonic function outside
is a subharmonic function outside 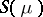 . For all
. For all  the Riesz potential
the Riesz potential 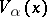 is a lower semi-continuous function on
is a lower semi-continuous function on  , continuous outside
, continuous outside 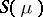 .
.
Among the general properties of Riesz potentials the following are the most important. The continuity principle: If 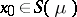 and if the restriction
and if the restriction  is continuous at the point
is continuous at the point  , then
, then  is continuous at
is continuous at 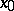 as a function on
as a function on 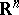 . The restricted maximum principle: If
. The restricted maximum principle: If  , then
, then  everywhere on
everywhere on 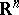 . When
. When 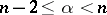 , a more precise maximum principle is valid: If
, a more precise maximum principle is valid: If 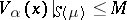 , then
, then 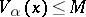 everywhere on
everywhere on 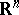 (this statement remains valid also when
(this statement remains valid also when  and
and  , that is, for the logarithmic potential).
, that is, for the logarithmic potential).
The capacity theory for Riesz potentials can be constructed, for example, on the basis of the concept of the 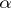 -energy of a measures
-energy of a measures  :
:
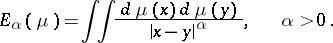 |
One may assume that for a compact set  ,
,
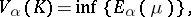 |
where the infimum is taken over all measures 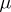 concentrated on
concentrated on 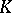 and such that
and such that 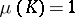 ; then the
; then the  -capacity is equal to
-capacity is equal to
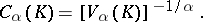 |
If  , then the infimum is attained on the capacitary measure
, then the infimum is attained on the capacitary measure  (also called equilibrium measure), which is concentrated on
(also called equilibrium measure), which is concentrated on  ,
, 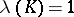 , generating the corresponding capacitary
, generating the corresponding capacitary  -potential
-potential 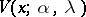 (cf. also Capacity potential). The further construction of
(cf. also Capacity potential). The further construction of  -capacities of arbitrary sets is carried out in the same way as for the classical capacities.
-capacities of arbitrary sets is carried out in the same way as for the classical capacities.
The Riesz potential is called after M. Riesz (see [2]), who obtained a number of important properties of Riesz potentials; for the first time such potentials were studied by O. Frostman (see [1]).
References
| [1] | O. Frostman, "Potentiel d'equilibre et capacité des ensembles avec quelques applications à la théorie des fonctions" Medd. Lunds Univ. Mat. Sem. , 3 (1935) pp. 1–118 |
| [2] | M. Riesz, "Intégrales de Riemann–Liouville et potentiels" Acata Sci. Math. Szeged , 9 (1938) pp. 1–42 |
| [3] | N.S. Landkof, "Foundations of modern potential theory" , Springer (1972) (Translated from Russian) |
| [4] | W.K. Hayman, P.B. Kennedy, "Subharmonic functions" , 1 , Acad. Press (1976) |
Comments
For  even and
even and  ,
,  is a fundamental solution of the polyharmonic equation
is a fundamental solution of the polyharmonic equation  , otherwise
, otherwise  is a fundamental solution. Riesz potentials are used in the theory of elliptic differential equations of order
is a fundamental solution. Riesz potentials are used in the theory of elliptic differential equations of order  , see [a2]. A treatment of Riesz potentials in the framework of balayage spaces is given in [a1].
, see [a2]. A treatment of Riesz potentials in the framework of balayage spaces is given in [a1].
The Riesz kernels  are the standard examples of convolution kernels. Thus, Riesz potentials may be regarded as special singular integrals. For more details on this interesting point of view see [a3].
are the standard examples of convolution kernels. Thus, Riesz potentials may be regarded as special singular integrals. For more details on this interesting point of view see [a3].
References
| [a1] | J. Bliedtner, W. Hansen, "Potential theory. An analytic and probabilistic approach to balayage" , Springer (1986) |
| [a2] | B.W. Schulze, G. Wildenhain, "Methoden der Potentialtheorie für elliptische Differentialgleichungen beliebiger Ordnung" , Birkhäuser (1977) |
| [a3] | E.M. Stein, "Singular integrals and differentiability properties of functions" , Princeton Univ. Press (1970) |
| [a4] | L. Carleson, "Selected problems on exceptional sets" , v. Nostrand (1967) |
Riesz potential. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Riesz_potential&oldid=14705