Riesz operator
The Riesz operators on a Banach space are, roughly speaking, those bounded linear operators that have a Riesz spectral theory, i.e. that have a spectral theory like that of compact operators, [a8] (see also Spectral theory of compact operators).
The precise definition is as follows ([a2], [a5]). Let 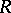 be a bounded operator on a Banach space
be a bounded operator on a Banach space 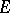 , and let
, and let 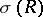 be the spectrum of
be the spectrum of 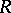 . A point
. A point 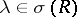 is isolated if
is isolated if 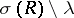 is closed in
is closed in 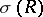 , i.e. if there is an open subset
, i.e. if there is an open subset 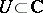 such that
such that 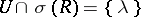 . A point
. A point 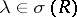 is a Riesz point if it is isolated and
is a Riesz point if it is isolated and 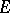 is the direct sum of a closed subspace
is the direct sum of a closed subspace 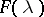 and a finite-dimensional subspace
and a finite-dimensional subspace 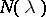 , both invariant under
, both invariant under 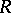 and such that
and such that 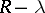 is nilpotent on
is nilpotent on 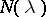 and a homeomorphism on
and a homeomorphism on 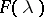 .
.
A bounded operator 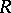 is a Riesz operator if all points
is a Riesz operator if all points 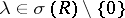 are Riesz points. Every compact operator is a Riesz operator (the Riesz theory of compact operators).
are Riesz points. Every compact operator is a Riesz operator (the Riesz theory of compact operators).
A bounded operator 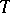 on
on  is called quasi-nilpotent if
is called quasi-nilpotent if 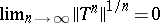 (which is equivalent to
(which is equivalent to 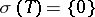 ).
).
A bounded operator 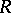 is a Riesz operator if and only if, [a3]:
is a Riesz operator if and only if, [a3]:
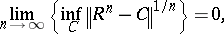 |
where 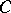 runs over all compact operators (see Compact operator).
runs over all compact operators (see Compact operator).
It is a long-standing question (still open as of 2000) whether every Riesz operator splits as the sum of a quasi-nilpotent operator and a compact operator. Such a decomposition is called a West decomposition, after T.T. West, who proved this for the case that  is a Hilbert space, [a6]. Further results can be found in [a1], [a7].
is a Hilbert space, [a6]. Further results can be found in [a1], [a7].
There is another, quite different, notion in which the phrase "Riesz operator" occurs, viz. the parametrized family of multiplier operators
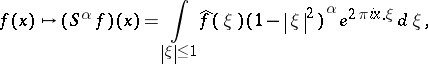 |
called the Bochner–Riesz operator, [a4]. They are important in Bochner–Riesz summability (see also Riesz summation method).
References
| [a1] | K.R. Davidson, D.A. Herrero, "Decomposition of Banach space operators" Indiana Univ. Math. J. , 35 (1986) pp. 333–343 |
| [a2] | J. Dieudonné, "Foundations of modern analysis" , Acad. Press (1960) pp. 323 |
| [a3] | A.F. Ruston, "Operators with a Fredholm theory" J. London Math. Soc. , 29 (1954) pp. 318–326 |
| [a4] | E.M. Stein, "Harmonic analysis: real-variable methods, orthogonality, and oscillatory integrals" , Princeton Univ. Press (1993) pp. 389 |
| [a5] | T.T. West, "Riesz operators in Banach spaces" Proc. London Math. Soc. , 16 (1966) pp. 131–140 |
| [a6] | T.T. West, "The decomposition of Riesz operators" Proc. London Math. Soc. , 16 (1966) pp. 737–752 |
| [a7] | H. Zhong, "On B-convex spaces and West decomposition of Riesz operators on them" Acta Math. Sinica , 37 (1994) pp. 563–569 |
| [a8] | H.R. Dowson, "Spectral theory of linear operators" , Acad. Press (1978) pp. 67ff. |
Riesz operator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Riesz_operator&oldid=15754