Riesz decomposition theorem

There are two different theorems that go by this name.

Riesz decomposition theorem for super- or subharmonic functions.

Roughly speaking, this asserts that a super- or subharmonic function is the sum of a potential and a harmonic function. For precise statements, see Subharmonic function (where it is called the Riesz local representation theorem), and Riesz theorem (where it is simply called the Riesz theorem), [a12], [a20]. See also [a8], 1.IV.8–9, 1.IX.11, 1.XIV.9, and [a8], 1.XV.7, 1.XVII.7, for a corresponding result for superparabolic functions. In [a4] the decomposition formula is called the Riesz integral representation and Riesz representation of a superharmonic function

There is also an abstract version (see also Potential theory, abstract), dealing with harmonic spaces, which states (see [a5], Thm. 2.2.2, p. 38) that every superharmonic function on a harmonic space which has a subharmonic minorant may be written uniquely as the sum of a potential and a harmonic function. This harmonic function is the greatest hypo-harmonic minorant of and is the infimum of any Perron set generated by .

An immediate consequence is the Brelot–Bauer theorem ([a5], Corol. 2.2.1, p. 38) that the real vector space of differences of positive harmonic functions on a harmonic space is a conditionally complete vector lattice (Riesz space) with respect to the natural order (i.e., pointwise comparison). This gives a link with the Riesz decomposition property.

There is also a converse Riesz decomposition theorem, [a11].

In the mid-1950s, the pioneering work of J.L. Doob and G.A. Hunt, [a7], [a14], [a15], [a16], showed a deep connection between potential theory and stochastic processes. Correspondingly, there are probabilistic Riesz decomposition theorems on decompositions of excessive functions, excessive measures and super-martingales. See [a3], [a9], [a8], 2.III.21, for precise formulations. There are also versions of these on commutative and non-commutative groups, [a1], [a2], [a6].

Riesz decomposition theorem for operators.

This theorem is also called the Riesz splitting theorem and deals with splitting the spectrum of an operator. Following [a10], p. 9ff, let be a bounded linear operator on a Banach space with spectrum . Let be an isolated part of , i.e. and 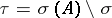are both closed in . Let

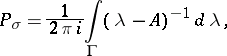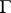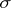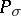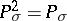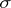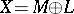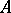where is a contour in the resolvent set of with in its interior and separating from . Then is a projection (i.e. ), called the Riesz projection or Riesz projector (cf. also Spectral synthesis (for a single point) and Krein space). Put , . Then , both and are invariant under , and , .

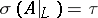If, moreover, 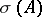is the disjoint union of two closed subsets 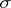and , then , .

For more general results (for closed linear operators), see [a10], p. 326ff. See also Functional calculus (particularly the part dealing with the Riesz–Dunford functional calculus) and, e.g., [a13].

F. Riesz himself, to whom the original result is due, called it the Zerlegungssatz.

References

[a1]	M. Banalescu, "On the Riesz decomposition property" Rev. Roum. Math. Pures Appl. , 36 (1991) pp. 107–114
[a2]	Ch. Berg, G. Frost, "Potential theory on locally compact Abelian groups" , Springer (1975) pp. 148
[a3]	R.M. Blumenthal, R.K. Getoor, "Markov processes and potential theory" , Acad. Press (1968) pp. 272, Thm. 2.11
[a4]	M. Brelot, "On topologies and boundaries in potential theory" , Springer (1971) pp. 93; 45
[a5]	C. Constantinescu, A. Cornea, "Potential theory on harmonic spaces" , Springer (1972)
[a6]	J. Deny, "Noyaux de convolution de Hunt et noyaux associes à une famille fondamentale" Ann. Inst. Fourier (Grenoble) , 12 (1962) pp. 643–667
[a7]	J.L. Doob, "Semimartingales and subharmonic functions" Trans. Amer. Math. Soc. , 77 (1954) pp. 86–121
[a8]	J.L. Doob, "Classical potential theory and its probabilistic counterpart" , Springer (1984)
[a9]	R.K. Getoor, J. Glover, "Riesz decompositions in Markov process theory" Trans. Amer. Math. Soc. , 285 (1984) pp. 107–132
[a10]	I. Gohberg, S. Goldberg, M.A. Kaashoek, "Classes of linear operators" , I , Birkhäuser (1990)
[a11]	M. Goldstein, W.H. Ow, "A converse of the Riesz decomposition theorem for harmonic spaces" Math. Z. , 173 (1980) pp. 105–109
[a12]	W.K. Hayman, P.B. Kennedy, "Subharmonic functions" , I , Acad. Press (1976) pp. Sect. 3.5
[a13]	E. Hille, "Methods in classical and functional analysis" , Addison-Wesley (1972) pp. 349–350
[a14]	G.A. Hunt, "Markoff processes and potentials I" Illinois J. Math. , 1 (1957) pp. 44–93
[a15]	G.A. Hunt, "Markoff processes and potentials II" Illinois J. Math. , 1 (1957) pp. 316–369
[a16]	G.A. Hunt, "Markoff processes and potentials III" Illinois J. Math. , 2 (1958) pp. 151–213
[a17]	F. Riesz, "Sur les fonctions subharmoniques et leur rapport à la theorie du potentiel I" Acta Math. , 48 (1926) pp. 329–343
[a18]	F. Riesz, "Sur les fonctions subharmoniques et leur rapport à la theorie du potentiel II" Acta Math. , 54 (1930) pp. 321–360
[a19]	F. Riesz, "Über die linearen Transformationen des komplexen Hilbertschen Raumes" Acta Sci. Math. (Szeged) , 5 (1930/32) pp. 23–54
[a20]	E.B. Saff, V. Totik, "Logarithmic potentials and external fields" , Springer (1997) pp. 100