Riesz decomposition property

Let be a partially ordered vector space, [a5], i.e. is a real vector space with a convex cone defining the partial order by if and only if . For , the corresponding interval is .

The (partially) ordered vector space has the Riesz decomposition property if for all , or, equivalently, if for all , .

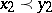A Riesz space (or vector lattice) automatically has the Riesz decomposition property.

Terminology on this concept varies a bit: in [a2] the property is referred to as the dominated decomposition property, while in [a3] it is called the decomposition property of F. Riesz.

The Riesz decomposition property and the Riesz decomposition theorem are quite different (although there is a link) and, in fact, the property does turn up as an axiom used in axiomatic potential theory (see also Potential theory, abstract), see [a1], where it is called the axiom of natural decomposition.

There is a natural non-commutative generalization to the setting of -algebras, as follows, [a4]. Let , , 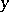be elements of a -algebra . If , then there are such that 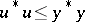, 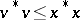and .

References

[a1]	C. Constantinescu, A. Cornea, "Potential theory on harmonic spaces" , Springer (1972) pp. 104
[a2]	W.A.J. Luxemburg, A.C. Zaanen, "Riesz spaces" , I , North-Holland (1971) pp. 73
[a3]	P. Meyer-Nieberg, "Banach lattices" , Springer (1971) pp. 3, Thm. 1.1.1
[a4]	G.K. Pedersen, "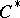-algebras and their automorphism groups" , Acad. Press (1979) pp. 14
[a5]	Y.-Ch. Wong, K.-F. Ng, "Partially ordered topological vector spaces" , Oxford Univ. Press (1973) pp. 9