Riemannian domain
Riemann domain, complex (-analytic) manifold over 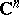
An analogue of the Riemann surface of an analytic function 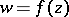 of a single complex variable
of a single complex variable  for the case of analytic functions
for the case of analytic functions 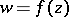 ,
, 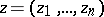 , of several complex variables
, of several complex variables  ,
, 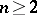 .
.
More precisely, a path-connected Hausdorff space 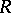 is called an (abstract) Riemann domain if there is a local homeomorphism (a projection)
is called an (abstract) Riemann domain if there is a local homeomorphism (a projection) 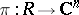 such that for each point
such that for each point 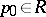 there is a neighbourhood
there is a neighbourhood 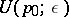 that transforms homeomorphically into a polydisc
that transforms homeomorphically into a polydisc
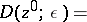 |
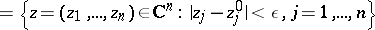 |
in the complex space 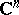 . A Riemann domain is a separable space.
. A Riemann domain is a separable space.
A complex function 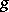 is called holomorphic on
is called holomorphic on 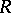 if for any point
if for any point 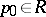 the function
the function 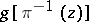 of
of  complex variables
complex variables  is holomorphic in the corresponding polydisc
is holomorphic in the corresponding polydisc 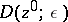 . The projection
. The projection 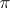 is given by the choice of
is given by the choice of  holomorphic functions
holomorphic functions 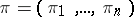 , which correspond to coordinates
, which correspond to coordinates  in
in 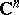 . Starting from a given regular element of an analytic function
. Starting from a given regular element of an analytic function 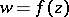 , its Riemann domain is constructed in the same way as the Riemann surface of a given analytic function of one complex variable, i.e. initially by means of analytic continuation one constructs the complete analytic function
, its Riemann domain is constructed in the same way as the Riemann surface of a given analytic function of one complex variable, i.e. initially by means of analytic continuation one constructs the complete analytic function 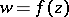 , and then, using neighbourhoods, one introduces a topology into the set of elements of the complete analytic function. Like Riemann surfaces, Riemann domains arise unavoidably in connection with analytic continuation of a given element of an analytic function when, following the ideas of B. Riemann, one tries to represent the complete analytic function
, and then, using neighbourhoods, one introduces a topology into the set of elements of the complete analytic function. Like Riemann surfaces, Riemann domains arise unavoidably in connection with analytic continuation of a given element of an analytic function when, following the ideas of B. Riemann, one tries to represent the complete analytic function 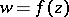 as a single-valued point function on a domain.
as a single-valued point function on a domain.
In particular, Riemann domains arise as multi-sheeted domains of holomorphy of analytic functions of several complex variables. Oka's theorem states that a Riemann domain is a domain of holomorphy if and only if it is holomorphically convex (see Holomorphically-convex complex space).
Modern studies of Riemann domains are conducted within the framework of the general theory of analytic spaces. A generalization of the concept of a domain of holomorphy leads to Stein spaces (cf. Stein space).
References
| [1] | B.V. Shabat, "Introduction of complex analysis" , 2 , Moscow (1976) (In Russian) |
| [2] | R.C. Gunning, H. Rossi, "Analytic functions of several complex variables" , Prentice-Hall (1965) |
| [3] | L. Hörmander, "An introduction to complex analysis in several variables" , North-Holland (1973) |
Comments
The notion as presented above of a Riemann domain has been extended in several ways: Instead of 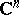 one may choose any (model) complex-analytic space
one may choose any (model) complex-analytic space 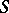 (cf. Complex space). An unramified Riemann domain over
(cf. Complex space). An unramified Riemann domain over 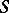 is a triple
is a triple 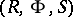 where
where 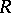 is a complex-analytic space and
is a complex-analytic space and 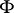 is a locally biholomorphic mapping from
is a locally biholomorphic mapping from 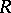 into
into 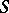 .
.
Next, a ramified Riemann domain over 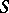 is a triple
is a triple 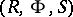 where again
where again 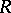 is a complex-analytic space and
is a complex-analytic space and 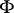 is now a discrete open holomorphic mapping from
is now a discrete open holomorphic mapping from 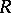 to
to 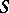 [a1].
[a1].
References
| [a1] | H. Behnke, P. Thullen, "Theorie der Funktionen meherer komplexer Veränderlichen" , Springer (1970) pp. Chapt. VI (Elraged & Revised Edition. Original: 1934) |
| [a2] | H. Grauert, K. Fritzsche, "Several complex variables" , Springer (1976) (Translated from German) |
Riemannian domain. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Riemannian_domain&oldid=12703