Riemann integral
A generalization of the concept of a Cauchy integral to a certain class of discontinuous functions; introduced by B. Riemann (1853). Let a function 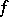 be given on an interval
be given on an interval 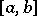 and let
and let 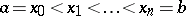 ,
, 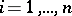 ,
, 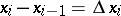 . The sum
. The sum
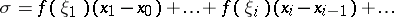 | (1) |
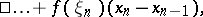 |
where 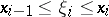 , is called the Riemann sum corresponding to the given subdivision of
, is called the Riemann sum corresponding to the given subdivision of 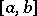 by the points
by the points 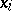 and to the sample of points
and to the sample of points 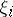 . The number
. The number 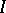 is called the limit of the Riemann sums (1) as
is called the limit of the Riemann sums (1) as 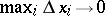 if for any
if for any 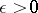 a
a 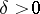 can be found such that
can be found such that 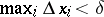 implies the inequality
implies the inequality 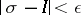 . If the Riemann sums have a finite limit
. If the Riemann sums have a finite limit 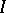 as
as 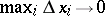 , then the function
, then the function 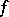 is called Riemann integrable over
is called Riemann integrable over 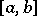 , where
, where 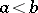 . The limit is known as the definite Riemann integral of
. The limit is known as the definite Riemann integral of 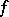 over
over 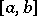 , and is written as
, and is written as
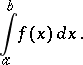 | (2) |
When 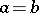 then, by definition,
then, by definition,
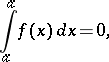 |
and when 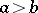 the integral (2) is defined using the equation
the integral (2) is defined using the equation
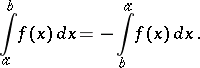 |
A necessary and sufficient condition for the Riemann integrability of 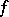 over
over 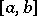 is the boundedness of
is the boundedness of 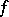 on this interval and the zero value of the Lebesgue measure of the set of all points of discontinuity of
on this interval and the zero value of the Lebesgue measure of the set of all points of discontinuity of 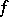 contained in
contained in 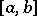 .
.
Properties of the Riemann integral.
1) Every Riemann-integrable function 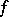 on
on 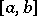 is also bounded on this interval (the converse is not true: The Dirichlet function is an example of a bounded and non-integrable function on
is also bounded on this interval (the converse is not true: The Dirichlet function is an example of a bounded and non-integrable function on 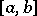 ).
).
2) The linearity property: For any constants 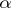 and
and 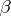 , the integrability over
, the integrability over 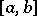 of both functions
of both functions 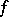 and
and 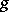 implies that the function
implies that the function 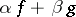 is integrable over this interval, and the equation
is integrable over this interval, and the equation
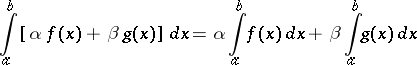 |
holds.
3) The integrability over 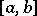 of both functions
of both functions 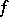 and
and 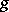 implies that their product
implies that their product 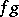 is integrable over this interval.
is integrable over this interval.
4) Additivity: The integrability of a function 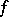 over both intervals
over both intervals 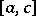 and
and 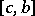 implies that
implies that 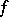 is integrable over
is integrable over 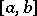 , and
, and
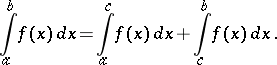 |
5) If two functions 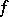 and
and 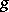 are integrable over
are integrable over 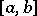 and if
and if 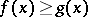 for every
for every  in this interval, then
in this interval, then
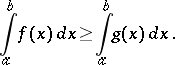 |
6) The integrability of a function 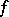 over
over 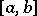 implies that the function
implies that the function 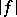 is integrable over this interval, and the estimate
is integrable over this interval, and the estimate
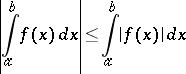 |
holds.
7) The mean-value formula: If two real-valued functions 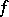 and
and 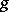 are integrable over
are integrable over 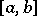 , if the function
, if the function 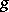 is non-negative or non-positive everywhere on this interval, and if
is non-negative or non-positive everywhere on this interval, and if 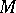 and
and 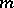 are the least upper and greatest lower bounds of
are the least upper and greatest lower bounds of 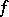 on
on 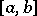 , then a number
, then a number 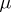 can be found,
can be found, 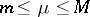 , such that the formula
, such that the formula
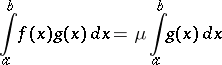 | (3) |
holds. If, in addition, 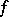 is continuous on
is continuous on 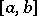 , then this interval will contain a point
, then this interval will contain a point 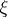 such that in formula (3),
such that in formula (3),
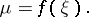 |
8) The second mean-value formula (Bonnet's formula): If a function 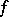 is real-valued and integrable over
is real-valued and integrable over 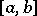 and if a function
and if a function 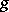 is real-valued and monotone on this interval, then a point
is real-valued and monotone on this interval, then a point 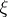 can be found in
can be found in 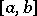 such that the formula
such that the formula
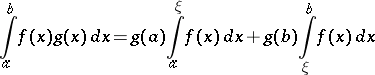 |
holds.
References
| [1] | B. Riemann, "Ueber die Darstellbarkeit einer Function durch eine trigonometrische Reihe" H. Weber (ed.) , B. Riemann's Gesammelte Mathematische Werke , Dover, reprint (1953) pp. 227–271 ((Original: Göttinger Akad. Abh.  (1868))) (1868))) |
| [2] | V.A. Il'in, E.G. Poznyak, "Fundamentals of mathematical analysis" , 1–2 , MIR (1982) (Translated from Russian) |
| [3] | L.D. Kudryavtsev, "A course in mathematical analysis" , 1–2 , Moscow (1988) (In Russian) |
| [4] | S.M. Nikol'skii, "A course of mathematical analysis" , 1–2 , MIR (1977) (Translated from Russian) |
Comments
References
| [a1] | G.E. Shilov, "Mathematical analysis" , 1–2 , M.I.T. (1974) (Translated from Russian) |
| [a2] | I.N. Pesin, "Classical and modern integration theories" , Acad. Press (1970) (Translated from Russian) |
| [a3] | K.R. Stromberg, "Introduction to classical real analysis" , Wadsworth (1981) |
| [a4] | W. Rudin, "Principles of mathematical analysis" , McGraw-Hill (1976) pp. 75–78 |
Riemann integral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Riemann_integral&oldid=13576