Resultant
of two polynomials 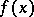 and
and 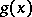
The element of the field 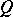 defined by the formula:
defined by the formula:
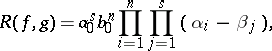 | (1) |
where 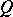 is the splitting field of the polynomial
is the splitting field of the polynomial 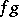 (cf. Splitting field of a polynomial), and
(cf. Splitting field of a polynomial), and 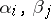 are the roots (cf. Root) of the polynomials
are the roots (cf. Root) of the polynomials
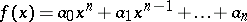 |
and
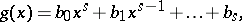 |
respectively. If 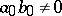 , then the polynomials have a common root if and only if the resultant equals zero. The following equality holds:
, then the polynomials have a common root if and only if the resultant equals zero. The following equality holds:
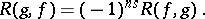 |
The resultant can be written in either of the following ways:
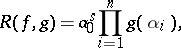 | (2) |
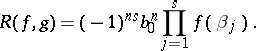 | (3) |
The expressions (1)–(3) are inconvenient for computing the resultant, since they contain the roots of the polynomials. Using the coefficients of the polynomials, the resultant can be expressed in the form of the following determinant of order 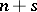 :
:
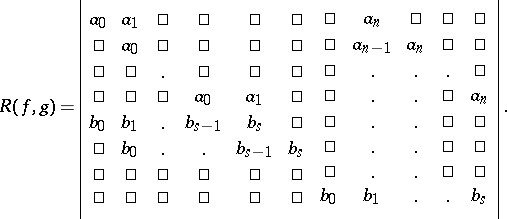 | (4) |
This determinant contains in the first  rows the coefficients of the polynomial
rows the coefficients of the polynomial 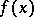 , and in the last
, and in the last  rows the coefficients of the polynomial
rows the coefficients of the polynomial 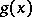 , and in the free spaces there are zeros.
, and in the free spaces there are zeros.
The resultant of two polynomials 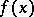 and
and 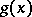 with numerical coefficients can be represented in the form of a determinant of order
with numerical coefficients can be represented in the form of a determinant of order  (or
(or  ). For this one has to find the remainders from the division of
). For this one has to find the remainders from the division of 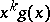 by
by 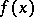 ,
, 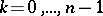 . Let these be
. Let these be
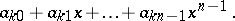 |
Then
 |
The discriminant 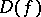 of the polynomial
of the polynomial
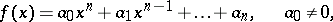 |
can be expressed by the resultant of the polynomial 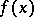 and its derivative
and its derivative 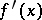 in the following way:
in the following way:
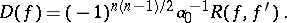 |
Application to solving a system of equations.
Let there be given a system of two algebraic equations with coefficients from a field 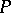 :
:
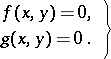 | (5) |
The polynomials 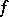 and
and 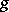 are written as polynomials in
are written as polynomials in  :
:
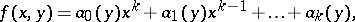 |
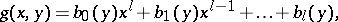 |
and according to formula (4) the resultant of these polynomials (as polynomials in  ) is calculated. This yields a polynomial that depends only on
) is calculated. This yields a polynomial that depends only on  :
:
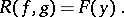 |
One says that the polynomial  is obtained by eliminating
is obtained by eliminating  from the polynomials
from the polynomials 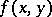 and
and 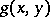 . If
. If 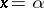 and
and 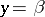 is a solution of the system (5), then
is a solution of the system (5), then 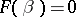 , and, conversely, if
, and, conversely, if 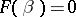 , then either the polynomials
, then either the polynomials 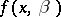 or
or 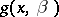 have a common root (which must be looked for among the roots of their greatest common divisor), or
have a common root (which must be looked for among the roots of their greatest common divisor), or 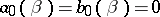 . Solving system (5) is thereby reduced to the computation of the roots of the polynomial
. Solving system (5) is thereby reduced to the computation of the roots of the polynomial 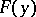 and of the common roots of the polynomials
and of the common roots of the polynomials 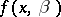 and
and 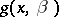 in one indeterminate.
in one indeterminate.
By analogy, systems of equations with any number of unknowns can be solved; however, this problem leads to extremely cumbersome calculations (see also Elimination theory).
References
| [1] | A.G. Kurosh, "Higher algebra" , MIR (1972) (Translated from Russian) |
| [2] | L.Ya. Okunev, "Higher algebra" , Moscow-Leningrad (1979) (In Russian) |
| [3] | B.L. van der Waerden, "Algebra" , 1–2 , Springer (1967–1971) (Translated from German) |
| [4] | W.V.D. Hodge, D. Pedoe, "Methods of algebraic geometry" , 1–3 , Cambridge Univ. Press (1947–1954) |
Comments
References
| [a1] | S. Lang, "Algebra" , Addison-Wesley (1984) |
Resultant. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Resultant&oldid=15841