Resolvent
A resolvent of an algebraic equation 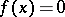 of degree
of degree  is an algebraic equation
is an algebraic equation 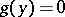 , with coefficients that rationally depend on the coefficients of
, with coefficients that rationally depend on the coefficients of 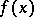 , such that, if the roots of this equation are known, the roots of the given equation
, such that, if the roots of this equation are known, the roots of the given equation 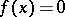 can be found by solving simpler equations of degrees not exceeding
can be found by solving simpler equations of degrees not exceeding  . A rational expression
. A rational expression  itself is sometimes called a resolvent.
itself is sometimes called a resolvent.
Let 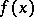 be a separable polynomial over a field
be a separable polynomial over a field  with Galois group
with Galois group 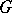 , and let
, and let 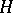 be a normal subgroup of
be a normal subgroup of 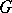 . Let
. Let 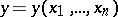 be a rational expression in
be a rational expression in  that remains invariant under all permutations of the roots
that remains invariant under all permutations of the roots  belonging to
belonging to 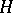 , and let
, and let 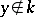 . Then
. Then 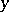 is a root of some equation
is a root of some equation 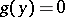 with coefficients from
with coefficients from 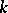 , the Galois group of which is a proper quotient group of
, the Galois group of which is a proper quotient group of 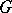 . Thus, solving the equation
. Thus, solving the equation 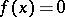 reduces to solving the equation
reduces to solving the equation 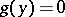 and solving the equation
and solving the equation 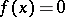 over the field
over the field 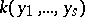 .
.
For example, in order to solve an equation of degree 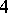 :
:
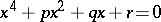 |
(every equation of degree 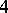 is reducible to this form), the following cubic resolvent is used:
is reducible to this form), the following cubic resolvent is used:
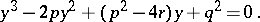 |
Its roots 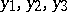 are related to the roots
are related to the roots 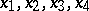 by the relations
by the relations 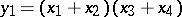 ,
, 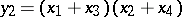 ,
, 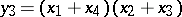 . The roots
. The roots 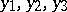 are determined by the Cardano formula, which also makes it possible to determine
are determined by the Cardano formula, which also makes it possible to determine 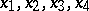 .
.
Successive application of the resolvent method permits one to solve any equation with a solvable Galois group by reduction to solving a chain of equations with cyclic Galois groups. Lagrange's resolvent is used in solving the latter.
Let 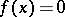 be an equation over a field
be an equation over a field 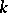 with a cyclic Galois group
with a cyclic Galois group 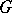 of order
of order  , and let
, and let 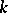 contain a primitive
contain a primitive  -th root of unity
-th root of unity 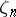 . For an element
. For an element 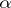 which belongs to the splitting field of the polynomial
which belongs to the splitting field of the polynomial 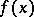 (cf. Splitting field of a polynomial), and for a character
(cf. Splitting field of a polynomial), and for a character 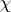 from
from 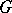 into the group of
into the group of  -th roots of unity, Lagrange's resolvent
-th roots of unity, Lagrange's resolvent 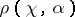 is defined by the formula:
is defined by the formula:
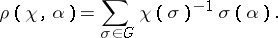 | (*) |
Let  be one of the roots of the polynomial
be one of the roots of the polynomial 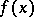 and let
and let 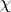 run through the characters of
run through the characters of 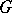 . Then for the system of linear equations (*) the roots
. Then for the system of linear equations (*) the roots  can be determined if the Lagrange resolvents are known for all characters
can be determined if the Lagrange resolvents are known for all characters 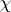 of
of 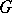 .
.
For 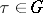 the relation
the relation
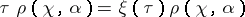 |
is fulfilled, showing that the elements 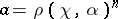 and
and 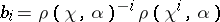 , for any integer
, for any integer 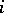 , are invariant under
, are invariant under 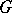 and are therefore uniquely defined rational expressions in the coefficients of the polynomial
and are therefore uniquely defined rational expressions in the coefficients of the polynomial 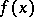 and the root
and the root 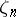 . If
. If 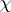 generates the group of characters of
generates the group of characters of  , then the following equalities hold:
, then the following equalities hold: 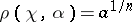 and
and 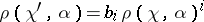 for
for 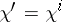 .
.
Any algebraic equation 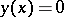 that is irreducible over a given field (see Galois theory) and that is such that as a result of the adjunction of one of its roots to this field a field is obtained that contains all roots of the equation
that is irreducible over a given field (see Galois theory) and that is such that as a result of the adjunction of one of its roots to this field a field is obtained that contains all roots of the equation  , is called a Galois resolvent of
, is called a Galois resolvent of 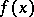 .
.
References
| [1] | B.L. van der Waerden, "Algebra" , 1–2 , Springer (1967–1971) (Translated from German) |
L.V. Kuz'min
The resolvent (resolvent kernel) of an integral equation
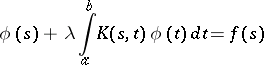 | (**) |
is understood to be a function 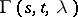 of the variables
of the variables  and the parameter
and the parameter 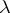 with the aid of which the solution of equation (**) can be represented in the form:
with the aid of which the solution of equation (**) can be represented in the form:
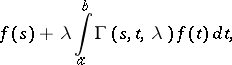 |
provided 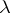 is not an eigenvalue of (**). For example, for the kernel
is not an eigenvalue of (**). For example, for the kernel 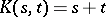 the resolvent is the function
the resolvent is the function
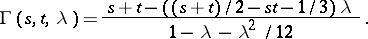 |
BSE-3
The resolvent of an operator 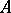 is an operator
is an operator 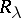 inverse to
inverse to  . Here
. Here 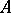 is a closed linear operator defined on a dense set
is a closed linear operator defined on a dense set 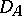 of a Banach space
of a Banach space 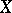 with values in the same space and
with values in the same space and 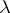 is such that
is such that 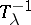 is a continuous linear operator on
is a continuous linear operator on 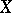 . The points
. The points  for which the resolvent exists are called regular points of
for which the resolvent exists are called regular points of 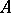 , and the collection of all regular points is the resolvent set
, and the collection of all regular points is the resolvent set 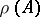 of this operator. The set
of this operator. The set 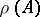 is open and on each of its connected components the operator
is open and on each of its connected components the operator 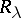 is an analytic function of the parameter
is an analytic function of the parameter  .
.
Properties of a resolvent are:
1)  for any two points
for any two points 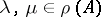 ;
;
2) 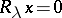 implies
implies 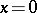 ;
;
3) if 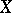 is a Hilbert space, then
is a Hilbert space, then 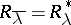 .
.
References
| [1] | K. Yosida, "Functional analysis" , Springer (1980) |
| [2] | N.I. [N.I. Akhiezer] Achieser, I.M. [I.M. Glaz'man] Glasman, "Theorie der linearen Operatoren im Hilbert Raum" , Akademie Verlag (1954) (Translated from Russian) |
| [3] | L.V. Kantorovich, G.P. Akilov, "Functional analysis in normed spaces" , Pergamon (1964) (Translated from Russian) |
Resolvent. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Resolvent&oldid=12785