Residually-finite group
A group that can be approximated by finite groups. Let 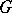 be a group and
be a group and 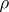 a relation (in other words, a predicate) between elements and sets of elements, defined on
a relation (in other words, a predicate) between elements and sets of elements, defined on 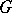 and all homomorphic images of it (for example, the binary relation of equality of elements, the binary relation "the element x belongs to the subgroup y" , the binary relation of conjugacy of elements, etc.). Let
and all homomorphic images of it (for example, the binary relation of equality of elements, the binary relation "the element x belongs to the subgroup y" , the binary relation of conjugacy of elements, etc.). Let  be a class of groups. One says that
be a class of groups. One says that  can be approximated by groups in
can be approximated by groups in  relative to
relative to 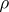 (or:
(or: 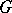 is residual in
is residual in 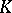 relative to
relative to 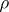 ) if for any elements and sets of elements of
) if for any elements and sets of elements of  that are not in relation
that are not in relation 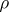 there is a homomorphism of
there is a homomorphism of 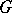 onto a group in
onto a group in  under which the images of these elements and sets are also not in relation
under which the images of these elements and sets are also not in relation  . Approximability relative to the relation of equality of elements is simply called approximability. A group can be approximated by groups in a class
. Approximability relative to the relation of equality of elements is simply called approximability. A group can be approximated by groups in a class 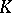 if and only if it is contained in a Cartesian product of groups in
if and only if it is contained in a Cartesian product of groups in  . Residual finiteness relative to
. Residual finiteness relative to  is denoted by
is denoted by 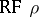 ; in particular, if
; in particular, if 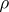 runs through the predicates of equality, conjugacy, belonging to a subgroup, belonging to a finitely-generated subgroup, etc., then one obtains the properties (and classes)
runs through the predicates of equality, conjugacy, belonging to a subgroup, belonging to a finitely-generated subgroup, etc., then one obtains the properties (and classes) 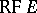 ,
, 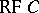 ,
, 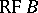 ,
, 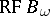 , etc. The presence of these properties in a group implies the solvability of the corresponding algorithmic problem.
, etc. The presence of these properties in a group implies the solvability of the corresponding algorithmic problem.
References
| [1] | M.I. Kargapolov, J.I. [Yu.I. Merzlyakov] Merzljakov, "Fundamentals of the theory of groups" , Springer (1979) (Translated from Russian) |
Comments
In outdated terminology a residually-finite group is called a finitely-approximated group, which is also the word-for-word translation of the Russian for this notion.
For a fuller account on residually-finite groups see [a1].
References
| [a1] | D.J.S. Robinson, "A course in the theory of groups" , Springer (1982) |
Residually-finite group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Residually-finite_group&oldid=12478