Representation of a group
A homomorphism of the group into the group of all invertible transformations of a set 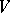 . A representation
. A representation 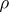 of a group
of a group 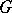 is called linear if
is called linear if  is a vector space over a field
is a vector space over a field 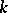 and if the transformations
and if the transformations  ,
, 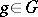 , are linear. Often, linear representations are, for shortness, simply termed representations (cf. Representation theory). In the theory of representations of abstract groups the theory of finite-dimensional representations of finite groups is best developed (cf. Finite group, representation of a; Representation of the symmetric groups).
, are linear. Often, linear representations are, for shortness, simply termed representations (cf. Representation theory). In the theory of representations of abstract groups the theory of finite-dimensional representations of finite groups is best developed (cf. Finite group, representation of a; Representation of the symmetric groups).
If 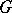 is a topological group, then one considers continuous linear representations of
is a topological group, then one considers continuous linear representations of 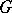 on a topological vector space
on a topological vector space 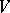 (cf. Continuous representation; Representation of a topological group). If
(cf. Continuous representation; Representation of a topological group). If 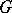 is a Lie group and
is a Lie group and 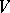 is a finite-dimensional space over
is a finite-dimensional space over 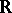 or
or 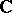 , then a continuous linear representation is automatically real analytic. Analytic and differentiable representations of a Lie group are defined also in the infinite-dimensional case (cf. Analytic representation; Infinite-dimensional representation). To each differentiable representation
, then a continuous linear representation is automatically real analytic. Analytic and differentiable representations of a Lie group are defined also in the infinite-dimensional case (cf. Analytic representation; Infinite-dimensional representation). To each differentiable representation 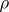 of a Lie group
of a Lie group  corresponds some linear representation of its Lie algebra — the differential representation of
corresponds some linear representation of its Lie algebra — the differential representation of  (cf. Representation of a Lie algebra). If
(cf. Representation of a Lie algebra). If 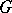 is moreover connected, then its finite-dimensional representations are completely determined by their differentials. The most developed branch of the representation theory of topological groups is the theory of finite-dimensional linear representations of semi-simple Lie groups, which is often formulated in the language of Lie algebras (cf. Finite-dimensional representation; Representation of the classical groups; Cartan theorem on the highest weight vector), the representation theory of compact groups, and the theory of unitary representations (cf. Representation of a compact group; Unitary representation).
is moreover connected, then its finite-dimensional representations are completely determined by their differentials. The most developed branch of the representation theory of topological groups is the theory of finite-dimensional linear representations of semi-simple Lie groups, which is often formulated in the language of Lie algebras (cf. Finite-dimensional representation; Representation of the classical groups; Cartan theorem on the highest weight vector), the representation theory of compact groups, and the theory of unitary representations (cf. Representation of a compact group; Unitary representation).
For algebraic groups one has the theory of rational representations (cf. Rational representation), which is in many aspects analogous to the theory of finite-dimensional representations of Lie groups.
References
| [1] | D.P. Zhelobenko, "Compact Lie groups and their representations" , Amer. Math. Soc. (1973) (Translated from Russian) |
| [2] | A.A. Kirillov, "Elements of the theory of representations" , Springer (1976) (Translated from Russian) |
| [3] | M.A. Naimark, "Theory of group representations" , Springer (1982) (Translated from Russian) |
| [4] | D.P. Zhelobenko, A.I. Shtern, "Representations of Lie groups" , Moscow (1981) (In Russian) |
Comments
References
| [a1] | D.J. Benson, "Modular representation theory: New trends and methods" , Lect. notes in math. , 1081 , Springer (1984) |
| [a2] | C.W. Curtis, I. Reiner, "Methods of representation theory" , 1–2 , Wiley (Interscience) (1981–1987) |
| [a3] | W. Feit, "The representation theory of finite groups" , North-Holland (1982) |
| [a4] | J.-P. Serre, "Linear representations of finite groups" , Springer (1977) (Translated from French) |
| [a5] | B. Huppert, "Endliche Gruppen" , 1 , Springer (1967) pp. 64 |
| [a6] | A.W. Knapp, "Representation theory of semisimple groups" , Princeton Univ. Press (1986) |
| [a7] | J. Tits, "Tabellen zu den einfachen Lie Grupppen und ihren Darstellungen" , Lect. notes in math. , 40 , Springer (1967) |
| [a8] | G. Warner, "Harmonic analysis on semisimple Lie groups" , 1–2 , Springer (1972) |
Representation of a group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Representation_of_a_group&oldid=15252