Representation of a Lie algebra
in a vector space 
A homomorphism  of a Lie algebra
of a Lie algebra  over a field
over a field  into the algebra
into the algebra  of all linear transformations of
of all linear transformations of  over
over  . Two representations
. Two representations  and
and  are called equivalent (or isomorphic) if there is an isomorphism
are called equivalent (or isomorphic) if there is an isomorphism 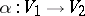 for which
for which
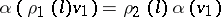 |
for arbitrary  ,
, 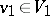 . A representation
. A representation 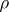 in
in 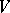 is called finite-dimensional if
is called finite-dimensional if  , and irreducible if there are no subspaces in
, and irreducible if there are no subspaces in 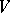 , distinct from the null subspace and all of
, distinct from the null subspace and all of  , that are invariant under all operators
, that are invariant under all operators 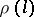 ,
, 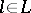 .
.
For given representations 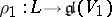 and
and 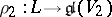 one constructs the representations
one constructs the representations  (the direct sum) and
(the direct sum) and  (the tensor product) of
(the tensor product) of  into
into  and
and 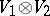 , by putting
, by putting
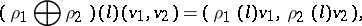 |
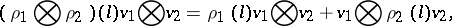 |
where 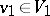 ,
, 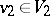 ,
,  . If
. If 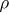 is a representation of
is a representation of  in
in  , then the formula
, then the formula
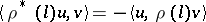 |
defines a representation  of
of 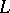 in the space dual to
in the space dual to 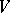 ; it is called the contragredient representation with respect to
; it is called the contragredient representation with respect to 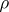 .
.
Every representation of 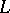 can be uniquely extended to a representation of the universal enveloping algebra
can be uniquely extended to a representation of the universal enveloping algebra 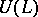 ; this gives an isomorphism between the category of representations of
; this gives an isomorphism between the category of representations of 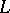 and the category of modules over
and the category of modules over 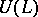 . In particular, to a representation
. In particular, to a representation 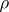 of
of 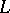 corresponds the ideal
corresponds the ideal  in
in 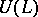 — the kernel of the extension
— the kernel of the extension  . If
. If 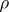 is irreducible,
is irreducible, 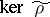 is a primitive ideal. Conversely, every primitive ideal in
is a primitive ideal. Conversely, every primitive ideal in 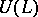 can be obtained in this manner from an (in general, non-unique) irreducible representation
can be obtained in this manner from an (in general, non-unique) irreducible representation  of
of 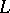 . The study of the space
. The study of the space 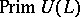 of primitive ideals, endowed with the Jacobson topology, is an essential part of the representation theory of Lie algebras. It has been studied completely in case
of primitive ideals, endowed with the Jacobson topology, is an essential part of the representation theory of Lie algebras. It has been studied completely in case  is a finite-dimensional solvable algebra and
is a finite-dimensional solvable algebra and 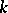 is an algebraically closed field of characteristic zero (cf. [2]).
is an algebraically closed field of characteristic zero (cf. [2]).
Finite-dimensional representations of finite-dimensional Lie algebras over an algebraically closed field of characteristic zero have been studied most extensively [6], [3], [5]. When the field is 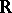 or
or  , these representations are in one-to-one correspondence with the analytic finite-dimensional representations of the corresponding simply-connected (complex or real) Lie group. In this case every representation of a solvable Lie algebra contains a one-dimensional invariant subspace (cf. Lie theorem). Any representation of a semi-simple Lie algebra is totally reduced, i.e. is isomorphic to a direct sum of irreducible representations. The irreducible representations of a semi-simple Lie algebra have been completely classified: the classes of isomorphic representations correspond one-to-one to the dominant weights; here, a weight, i.e. an element of the dual space
, these representations are in one-to-one correspondence with the analytic finite-dimensional representations of the corresponding simply-connected (complex or real) Lie group. In this case every representation of a solvable Lie algebra contains a one-dimensional invariant subspace (cf. Lie theorem). Any representation of a semi-simple Lie algebra is totally reduced, i.e. is isomorphic to a direct sum of irreducible representations. The irreducible representations of a semi-simple Lie algebra have been completely classified: the classes of isomorphic representations correspond one-to-one to the dominant weights; here, a weight, i.e. an element of the dual space 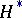 of a Cartan subalgebra
of a Cartan subalgebra  of
of 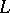 , is called dominant if its values on a canonical basis
, is called dominant if its values on a canonical basis 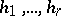 of
of  are non-negative integers (cf. Cartan theorem on the highest weight vector). For a description of the structure of an irreducible representation by its corresponding dominant weight (its highest weight) see Multiplicity of a weight; Character formula.
are non-negative integers (cf. Cartan theorem on the highest weight vector). For a description of the structure of an irreducible representation by its corresponding dominant weight (its highest weight) see Multiplicity of a weight; Character formula.
An arbitrary element (not necessarily a dominant weight) 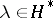 also determines an irreducible linear representation of a semi-simple Lie algebra
also determines an irreducible linear representation of a semi-simple Lie algebra  with highest weight
with highest weight 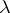 . This representation is, however, infinite-dimensional (cf. Representation with a highest weight vector). The corresponding
. This representation is, however, infinite-dimensional (cf. Representation with a highest weight vector). The corresponding  -modules are called Verma modules (cf. [2]). A complete classification of the irreducible infinite-dimensional representations of semi-simple Lie algebras has not yet been obtained (1991).
-modules are called Verma modules (cf. [2]). A complete classification of the irreducible infinite-dimensional representations of semi-simple Lie algebras has not yet been obtained (1991).
If 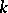 is an algebraically closed field of characteristic
is an algebraically closed field of characteristic  , then irreducible representations of a finite-dimensional Lie algebra
, then irreducible representations of a finite-dimensional Lie algebra 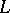 are always finite-dimensional and their dimensions are bounded by a constant depending on
are always finite-dimensional and their dimensions are bounded by a constant depending on 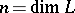 . If the algebra
. If the algebra  has a
has a 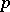 -structure (cf. Lie
-structure (cf. Lie  -algebra), then the constant is
-algebra), then the constant is 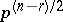 , where
, where  is the minimum possible dimension of an annihilator of a linear form on
is the minimum possible dimension of an annihilator of a linear form on  in the co-adjoint representation [4]. The following construction is used for the description of the set of irreducible representations in this case. Let
in the co-adjoint representation [4]. The following construction is used for the description of the set of irreducible representations in this case. Let 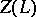 be the centre of
be the centre of  and let
and let 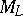 be the affine algebraic variety (of dimension
be the affine algebraic variety (of dimension 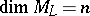 ) whose algebra of regular functions coincides with
) whose algebra of regular functions coincides with 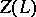 (a Zassenhaus variety). The mapping
(a Zassenhaus variety). The mapping  makes it possible to assign a point on the Zassenhaus variety to each irreducible representation. The mapping thus obtained is surjective, the pre-image of any point of
makes it possible to assign a point on the Zassenhaus variety to each irreducible representation. The mapping thus obtained is surjective, the pre-image of any point of 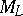 is finite and for the points of an open everywhere-dense subset this pre-image consists of one element [7]. A complete description of all irreducible representations has been obtained for nilpotent Lie algebras (cf. [8]) and certain individual examples (cf. [9], [10]). Most varied results have also been obtained for special types of representations.
is finite and for the points of an open everywhere-dense subset this pre-image consists of one element [7]. A complete description of all irreducible representations has been obtained for nilpotent Lie algebras (cf. [8]) and certain individual examples (cf. [9], [10]). Most varied results have also been obtained for special types of representations.
References
| [1] | N. Bourbaki, "Elements of mathematics. Lie groups and Lie algebras" , Addison-Wesley (1975) (Translated from French) |
| [2] | J. Dixmier, "Enveloping algebras" , North-Holland (1977) (Translated from French) |
| [3] | N. Jacobson, "Lie algebras" , Interscience (1962) ((also: Dover, reprint, 1979)) |
| [4] | A.A. Mil'ner, "Maximal degree of irreducible Lie algebra representations over a field of positive characteristic" Funct. Anal. Appl. , 14 : 2 (1980) pp. 136–137 Funkts. Anal. i Prilozhen. , 14 : 2 (1980) pp. 67–68 |
| [5] | J.-P. Serre, "Lie algebras and Lie groups" , Benjamin (1965) (Translated from French) |
| [6] | , Theórie des algèbres de Lie. Topologie des groupes de Lie , Sem. S. Lie , Ie année 1954–1955 , Secr. Math. Univ. Paris (1955) |
| [7] | H. Zassenhaus, "The representations of Lie algebras of prime characteristic" Proc. Glasgow Math. Assoc. , 2 (1954) pp. 1–36 |
| [8] | B.Yu. Veisfeiler, V.G. Kats, "Irreducible representations of Lie 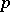 -algebras" Funct. Anal. Appl. , 5 : 2 (1971) pp. 111–117 Funkts. Anal. i Prilozhen. , 5 : 2 (1971) pp. 28–36 -algebras" Funct. Anal. Appl. , 5 : 2 (1971) pp. 111–117 Funkts. Anal. i Prilozhen. , 5 : 2 (1971) pp. 28–36 |
| [9] | J.C. Jantzen, "Zur Charakterformel gewisser Darstellungen halbeinfacher Gruppen und Lie-Algebren" Math. Z. , 140 : 1 (1974) pp. 127–149 |
| [10] | A.N. Rudakov, "On the representation of the classical Lie algebras in characteristic 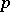 " Math. USSR Izv. , 4 (1970) pp. 741–749 Izv. Akad. Nauk SSSR Ser. Mat. , 34 : 4 (1970) pp. 735–743 " Math. USSR Izv. , 4 (1970) pp. 741–749 Izv. Akad. Nauk SSSR Ser. Mat. , 34 : 4 (1970) pp. 735–743 |
Comments
For a study of Prim 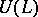 for semi-simple
for semi-simple 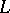 , see [a2].
, see [a2].
References
| [a1] | J.E. Humphreys, "Introduction to Lie algebras and representation theory" , Springer (1972) |
| [a2] | J.C. Jantzen, "Einhüllende Algebren halbeinfacher Lie-Algebren" , Springer (1983) |
Representation of a Lie algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Representation_of_a_Lie_algebra&oldid=12206