Removable set
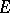 of points of the complex plane
of points of the complex plane 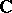 for a certain class
for a certain class 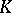 of functions analytic in a domain
of functions analytic in a domain 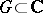
A compact set 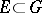 such that any function
such that any function 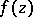 of class
of class 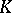 in
in 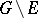 can be continued as a function of class
can be continued as a function of class  to the whole domain
to the whole domain 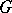 . The situation may be described in other words by saying that "the set E is set, removable for a class of functionsremovable for the class K" or that "E is a null-set for the class K" , briefly:
. The situation may be described in other words by saying that "the set E is set, removable for a class of functionsremovable for the class K" or that "E is a null-set for the class K" , briefly: 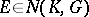 . It is assumed that the complement
. It is assumed that the complement 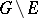 is a domain and that the class
is a domain and that the class 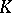 is defined for any domain.
is defined for any domain.
According to another definition, a set 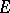 is removable for a class
is removable for a class 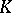 ,
, 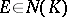 , if the fact that
, if the fact that 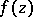 is a function of class
is a function of class 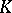 in the complement
in the complement 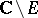 implies that
implies that 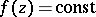 . Here the membership relations
. Here the membership relations  and
and 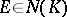 are generally speaking not equivalent.
are generally speaking not equivalent.
A first result on removable sets was the classical Cauchy–Riemann theorem on removable singularities: If a function 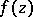 is analytic and bounded in a punctured neighbourhood
is analytic and bounded in a punctured neighbourhood 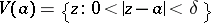 of a point
of a point 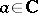 , then it can be continued analytically to
, then it can be continued analytically to  . A wider statement of the question (Painlevé's problem) is due to P. Painlevé: To find necessary and sufficient conditions on a set
. A wider statement of the question (Painlevé's problem) is due to P. Painlevé: To find necessary and sufficient conditions on a set 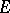 in order that
in order that 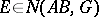 , where
, where 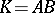 is the class of all bounded analytic functions (cf. [1]). Painlevé himself found a sufficient condition:
is the class of all bounded analytic functions (cf. [1]). Painlevé himself found a sufficient condition: 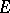 must have linear Hausdorff measure zero. Necessary and sufficient conditions for Painlevé's problem were obtained by L.V. Ahlfors (cf. [2]):
must have linear Hausdorff measure zero. Necessary and sufficient conditions for Painlevé's problem were obtained by L.V. Ahlfors (cf. [2]): 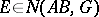 if and only if
if and only if 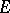 has zero analytic capacity. There exists an example of a set
has zero analytic capacity. There exists an example of a set 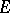 of positive length but zero analytic capacity. On removable sets for different classes of analytic functions of one complex variable and related unsolved problems see [3], [4], [6], [9].
of positive length but zero analytic capacity. On removable sets for different classes of analytic functions of one complex variable and related unsolved problems see [3], [4], [6], [9].
In the case of analytic functions 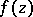 of several complex variables
of several complex variables 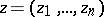 ,
, 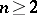 , the statement of the problem on removable sets is changed by virtue of the classical Osgood–Brown theorem: If
, the statement of the problem on removable sets is changed by virtue of the classical Osgood–Brown theorem: If 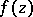 is a regular analytic function in a domain
is a regular analytic function in a domain 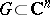 , except possibly on a compact set
, except possibly on a compact set 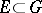 for which the complement
for which the complement 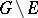 is connected, then
is connected, then 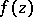 can be continued analytically to the whole domain
can be continued analytically to the whole domain 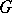 . For other theorems on removable sets for
. For other theorems on removable sets for 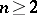 , as well as connections with the concept of a domain of holomorphy, see e.g. [7], [10].
, as well as connections with the concept of a domain of holomorphy, see e.g. [7], [10].
The problem of removable sets can also be posed for harmonic, subharmonic and other functions. E.g., let 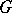 be a domain in Euclidean space
be a domain in Euclidean space 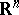 ,
, 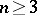 , let
, let 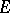 be compact,
be compact, 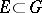 , let
, let 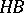 be the class of bounded harmonic functions, and let
be the class of bounded harmonic functions, and let 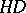 be the class of harmonic functions with finite Dirichlet integral. Then the membership relations
be the class of harmonic functions with finite Dirichlet integral. Then the membership relations 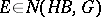 and
and 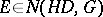 are equivalent and are valid if and only if the capacity of
are equivalent and are valid if and only if the capacity of 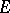 is zero (cf. [5], [8]).
is zero (cf. [5], [8]).
References
| [1] | L. Zoretti, "Leçons sur la prolongement analytique" , Gauthier-Villars (1911) |
| [2] | L.V. Ahlfors, "Bounded analytic functions" Duke Math. J. , 14 : 1 (1947) pp. 1–11 |
| [3] | K. Nohiro, "Cluster sets" , Springer (1960) |
| [4] | S.Ya. Khavinson, "Analytic functions of bounded type" Itogi Nauk. Mat. Anal. 1963 (1965) pp. 5–80 (In Russian) |
| [5] | L. Carleson, "Selected problems on exceptional sets" , v. Nostrand (1967) |
| [6] | M.S. Mel'nikov, S.O. Sinanyan, "Aspects of approximation theory for functions of one complex variable" J. Soviet Math. , 5 : 5 (1976) pp. 688–752 Itogi Nauk. i Tekhn. Sovremen. Probl. Mat. , 4 (1975) pp. 143–250 |
| [7] | B.V. Shabat, "Introduction of complex analysis" , 2 , Moscow (1985) (In Russian) |
| [8] | W.K. Hayman, P.B. Kennedy, "Subharmonic functions" , 1 , Acad. Press (1976) |
| [9] | E.P. Dolzhenko, "Elimination of singularities of analytic functions" Uspekhi Mat. Nauk , 18 : 4 (1963) pp. 135–142 (In Russian) |
| [10] | L.J. Riihentaus, "Removable singularities of analytic functions of several complex variables" Math. Z. , 158 (1978) pp. 45–54 |
Comments
The Osgood–Brown theorem is also called Hartogs' theorem, cf. Hartogs theorem.
See also Analytic continuation; Analytic set; Removable singular point.
For quite general continuation results see [a2]; Riemann's theorem has an analogue in 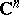 : Bounded analytic functions extend analytically across subvarieties of codimension
: Bounded analytic functions extend analytically across subvarieties of codimension 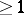 , while all analytic functions can be analytically continued across subvarieties of codimension
, while all analytic functions can be analytically continued across subvarieties of codimension 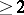 . See [a1].
. See [a1].
References
| [a1] | R.C. Gunning, H. Rossi, "Analytic functions of several complex variables" , Prentice-Hall (1965) pp. Chapt. 1, Section G |
| [a2] | R. Harvey, J. Polking, "Removable singularities of solutions of linear partial differential equations" Acta Math. , 125 (1970) pp. 39–55 |
| [a3] | J.B. Garnett, "Analytic capacity and measure" , Lect. notes in math. , 297 , Springer (1972) |
| [a4] | E.M. Chirka, "Complex analytic sets" , Kluwer (1989) (Translated from Russian) |
Removable set. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Removable_set&oldid=14994