Relative homological algebra
A homological algebra associated with a pair of Abelian categories  and a fixed functor
and a fixed functor  (cf. Abelian category). The functor
(cf. Abelian category). The functor  is taken to be additive, exact and faithful. A short exact sequence of objects of
is taken to be additive, exact and faithful. A short exact sequence of objects of  ,
,
 |
is said to be admissible if the exact sequence
 |
splits in 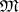 (cf. Split sequence). By means of the class
(cf. Split sequence). By means of the class  of admissible exact sequences, the class of
of admissible exact sequences, the class of  -projective (respectively,
-projective (respectively, 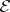 -injective) objects is defined as the class of those objects
-injective) objects is defined as the class of those objects 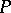 (respectively,
(respectively, 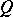 ) for which the functor
) for which the functor 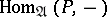 (respectively,
(respectively, 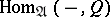 ) is exact on the admissible short exact sequences.
) is exact on the admissible short exact sequences.
Any projective object  of
of  is
is 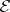 -projective, although this does not mean that in
-projective, although this does not mean that in 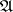 there are enough relative projective objects (i.e. that for any object
there are enough relative projective objects (i.e. that for any object 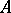 from
from  , an admissible epimorphism
, an admissible epimorphism 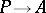 of a certain
of a certain 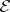 -projective object of
-projective object of 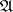 exists). If
exists). If  contains enough
contains enough  -projective or
-projective or  -injective objects, then the usual constructions of homological algebra make it possible to construct derived functors in this category, which are called relative derived functors.
-injective objects, then the usual constructions of homological algebra make it possible to construct derived functors in this category, which are called relative derived functors.
Examples. Let  be the category of
be the category of  -modules over an associative ring
-modules over an associative ring 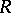 with a unit, let
with a unit, let  be the category of Abelian groups and let
be the category of Abelian groups and let  be the functor which "forgets" the module structure. In this case all exact sequences are admissible, and as a result the "absolute" (i.e. usual) homological algebra is obtained.
be the functor which "forgets" the module structure. In this case all exact sequences are admissible, and as a result the "absolute" (i.e. usual) homological algebra is obtained.
If  is a group, then every
is a group, then every 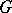 -module is, in particular, an Abelian group. If
-module is, in particular, an Abelian group. If  is an algebra over a commutative ring
is an algebra over a commutative ring 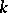 , then every
, then every 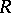 -module is a
-module is a 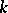 -module. If
-module. If 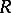 and
and  are rings and
are rings and  , then every
, then every 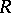 -module is an
-module is an 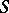 -module. In all these cases there is a functor from one Abelian category into the other defining the relative derived functors.
-module. In all these cases there is a functor from one Abelian category into the other defining the relative derived functors.
References
| [1] | S. MacLane, "Homology" , Springer (1963) |
| [2] | J.C. Moore, S. Eilenberg, "Foundations of relative homological algebra" , Amer. Math. Soc. (1965) |
Relative homological algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Relative_homological_algebra&oldid=15425