Relation
A subset of a finite Cartesian power  of a given set
of a given set  , i.e. a set of tuples
, i.e. a set of tuples  of
of  elements of
elements of  .
.
A subset  is called an
is called an  -place, or an
-place, or an  -ary, relation on
-ary, relation on 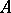 . The number
. The number  is called the rank, or type, of the relation
is called the rank, or type, of the relation  . A subset
. A subset  is also called an
is also called an  -place, or
-place, or  -ary, predicate on
-ary, predicate on 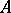 . The notation
. The notation 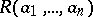 signifies that
signifies that 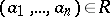 .
.
One-place relations are called properties. Two-place relations are called binary, three-place relations are called ternary, etc.
The set  and the empty subset
and the empty subset 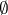 in
in 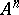 are called, respectively, the universal relation and the zero relation of rank
are called, respectively, the universal relation and the zero relation of rank  on
on 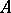 . The diagonal of the set
. The diagonal of the set 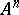 , i.e. the set
, i.e. the set
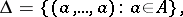 |
is called the equality relation on  .
.
If  and
and 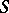 are
are  -place relations on
-place relations on 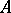 , then the following subsets of
, then the following subsets of 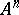 will also be
will also be  -place relations on
-place relations on 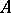 :
:
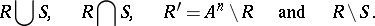 |
The set of all  -ary relations on
-ary relations on 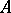 is a Boolean algebra relative to the operations
is a Boolean algebra relative to the operations 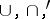 . An
. An 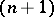 -place relation
-place relation  on
on  is called a function if for any elements
is called a function if for any elements  ,
, 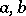 from
from  it follows from
it follows from 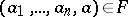 and
and 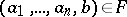 that
that  .
.
See also Binary relation; Correspondence.
Comments
References
| [a1] | J.L. Bell, M. Machover, "A course in mathematical logic" , North-Holland (1977) |
Relation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Relation&oldid=14950