Regularization method
A method for constructing approximate solutions of ill-posed problems in the following way: As approximate solution of an ill-posed problem (also called an incorrectly-posed problem) one takes the values of a regularizing operator with regard to the approximate nature of the initial data.
For the sake of being specific, consider the problem of finding the solution of a functional equation of the form 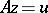 , in which
, in which  and
and  are elements of metric spaces
are elements of metric spaces 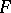 and
and 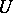 with distance functions
with distance functions 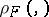 and
and 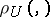 , respectively. If, for example,
, respectively. If, for example, 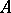 is a completely-continuous operator, then the solution of such an equation need not be stable with respect to small changes of the right-hand side
is a completely-continuous operator, then the solution of such an equation need not be stable with respect to small changes of the right-hand side  . Suppose that, instead of the exact values
. Suppose that, instead of the exact values 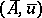 of the initial data, approximations
of the initial data, approximations 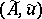 are given. In these circumstances one can only ask for approximations to the solution
are given. In these circumstances one can only ask for approximations to the solution  of the equation
of the equation 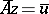 . As an approximate solution of an ill-posed problem of this type, with approximate initial data
. As an approximate solution of an ill-posed problem of this type, with approximate initial data 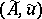 , one cannot take an exact solution of the equation
, one cannot take an exact solution of the equation 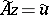 , since such a solution need not exist, and even if it does, it need not be stable with respect to small changes of the initial data, so that such a "solution" may not admit a physical interpretation. In what follows, it is assumed for simplicity that only the right-hand side
, since such a solution need not exist, and even if it does, it need not be stable with respect to small changes of the initial data, so that such a "solution" may not admit a physical interpretation. In what follows, it is assumed for simplicity that only the right-hand side  is approximate, and that the operator
is approximate, and that the operator 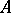 is specified exactly.
is specified exactly.
Let 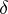 be a bound on the deviation of
be a bound on the deviation of 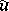 from
from 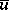 , that is, on the distance
, that is, on the distance 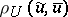 , and let
, and let 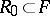 be a given class of possible solutions (comparison models). It is natural to search for approximate solutions of the equation
be a given class of possible solutions (comparison models). It is natural to search for approximate solutions of the equation 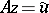 among the elements
among the elements 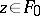 compatible with the initial data, that is, such that
compatible with the initial data, that is, such that 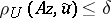 . Let
. Let 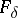 be the set of all such elements from
be the set of all such elements from 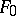 . If, in the chosen class
. If, in the chosen class 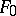 of possible solutions, there are no elements (for example, functions
of possible solutions, there are no elements (for example, functions 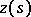 ) compatible with the initial data, then this means that the elements
) compatible with the initial data, then this means that the elements  have an over-simplified (too rough) structure. In this case it is necessary to extend
have an over-simplified (too rough) structure. In this case it is necessary to extend 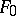 by taking, if necessary, an increasing sequences of classes
by taking, if necessary, an increasing sequences of classes 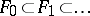 until a class
until a class 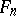 is reached that contains elements (for example, functions) that are compatible with the initial data.
is reached that contains elements (for example, functions) that are compatible with the initial data.
If 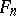 is not empty, then it may contain elements (functions) that are essentially different from one another. In such cases, the single requirement of compatibility of a possible solution with the initial data cannot serve as the only criterion for finding a well-defined approximate solution of the equation
is not empty, then it may contain elements (functions) that are essentially different from one another. In such cases, the single requirement of compatibility of a possible solution with the initial data cannot serve as the only criterion for finding a well-defined approximate solution of the equation 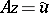 , as there are insufficient grounds for the choice of an approximate solution from among the compatible elements of
, as there are insufficient grounds for the choice of an approximate solution from among the compatible elements of 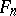 .
.
For stable solutions to be well-defined, one needs a certain principle for selecting solutions compatible with  . The formulation of this usually varies in accordance with the nature of the problem. Such a selection can be made, for example, on the principle of choosing an element (functions in
. The formulation of this usually varies in accordance with the nature of the problem. Such a selection can be made, for example, on the principle of choosing an element (functions in 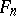 ) that has minimal complexity. The notion of complexity of an element
) that has minimal complexity. The notion of complexity of an element  can be formalized, for example, using complexity functionals
can be formalized, for example, using complexity functionals 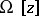 — continuous, non-negative functionals satisfying certain special requirements (see [1]). As a measure of the complexity of an element
— continuous, non-negative functionals satisfying certain special requirements (see [1]). As a measure of the complexity of an element  one takes the value of the functional
one takes the value of the functional 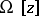 . Thus, if the elements
. Thus, if the elements  are continuous functions
are continuous functions  on an interval
on an interval 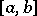 and belong to the class
and belong to the class 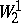 , then one can take the complexity functional
, then one can take the complexity functional 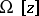 to be
to be
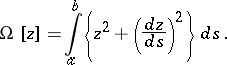 |
The search for approximate solutions of the equation 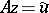 among the simplest elements (functions) that are compatible with the initial data leads to the problem of finding an element of
among the simplest elements (functions) that are compatible with the initial data leads to the problem of finding an element of 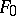 that minimizes
that minimizes 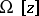 on
on 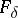 . If
. If 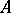 is a linear operator and if
is a linear operator and if 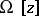 does not have local minima in its domain of definition
does not have local minima in its domain of definition 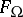 , then this problem can be reduced to that (see [1] for some details) of finding an element
, then this problem can be reduced to that (see [1] for some details) of finding an element 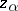 in the set
in the set 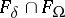 that minimizes the functional
that minimizes the functional
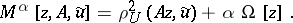 |
The value of the parameter 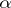 (the regularization parameter) must be chosen in accordance with the level of error in the initial data. For example, it can be defined in terms of discrepancy, that is, by the condition
(the regularization parameter) must be chosen in accordance with the level of error in the initial data. For example, it can be defined in terms of discrepancy, that is, by the condition 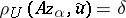 , for a given
, for a given 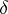 . But there are other ways of determining
. But there are other ways of determining 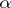 (see [1]). Thus,
(see [1]). Thus, 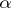 may depend on
may depend on 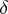 and
and 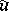 ,
, 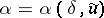 . The element
. The element 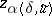 is then taken as an approximate solution of the equation
is then taken as an approximate solution of the equation 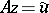 . This is also one of the forms of the regularization method developed in [2], [3]. In a similar way one can formulate approximate solutions of the equation
. This is also one of the forms of the regularization method developed in [2], [3]. In a similar way one can formulate approximate solutions of the equation 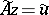 in case both
in case both 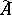 and
and 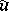 are approximately given. In this case a functional of the type
are approximately given. In this case a functional of the type 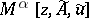 is minimized (see [1], for example). There are other possible forms of the regularization method, and applications to other classes of problems (see [1]). Regularization methods have also been developed for solving non-linear problems (see [1], [4]).
is minimized (see [1], for example). There are other possible forms of the regularization method, and applications to other classes of problems (see [1]). Regularization methods have also been developed for solving non-linear problems (see [1], [4]).
References
| [1] | A.N. Tikhonov, V.I. [V.I. Arsenin] Arsenine, "Solution of ill-posed problems" , Wiley (1977) (Translated from Russian) |
| [2] | A.N. Tikhonov, "Solution of incorrectly formulated problems and the regularization method" Soviet Math. Dokl. , 4 : 4 (1963) pp. 1035–1038 Dokl. Akad. Nauk SSSR , 151 : 3 (1963) pp. 501–504 |
| [3] | A.N. Tikhonov, "Regularization of incorrectly posed problems" Soviet Math. Dokl. , 4 : 6 (1963) pp. 1624–1627 Dokl. Akad. Nauk SSSR , 153 : 1 (1963) pp. 49–52 |
| [4] | M.M. [M.M. Lavrent'ev] Lavrentiev, "Some improperly posed problems of mathematical physics" , Springer (1967) (Translated from Russian) |
Comments
For other regularization methods and their convergence properties see (the editorial comments to) ill-posed problems. That article also contains a discussion of "inverse problems" arising in various applications giving rise to ill-posed problems, and many references. The spectral-theoretic methods discussed there also include some iterative methods. Another iterative method that can be considered as a regularization method is the conjugate gradient method (cf. Conjugate gradients, method of); it is discussed from this point of view in the articles by H. Brakhage and L. Louis in [a2] (see also [a6]). Convergence and convergence rates for Tikhonov regularization of non-linear ill-posed problems are considered in some papers in Volume  (1989) of the journal "Inverse Problems" , which in general contains many articles about regularization methods.
(1989) of the journal "Inverse Problems" , which in general contains many articles about regularization methods.
A different approach to regularization is based on statistical considerations (see [a1], [a5]) and is rooted in the method of ridge regression, [a4]. A well-known parameter choice strategy for statistical regularization is generalized cross-validation (see e.g. the article by G. Wahba in [a2] and the references quoted there).
For the use of reproducing-kernel Hilbert spaces in regularization see [a3] and [a7]. A practical comparison of various regularization methods is made in [a8].
References
| [a1] | M. Bertero, G. Viano, "On probabilistic methods for the solution of improperly posed problems" Boll. Un. Mat. Ital. , 15-B (1978) pp. 483–508 |
| [a2] | H.W. Engl (ed.) C.W. Groetsch (ed.) , Inverse and ill-posed problems , Acad. Press (1987) |
| [a3] | J. Hilgers, "On the equivalence of regularization and certain reproducing kernel Hilbert space approaches for solving first kind problems" SIAM J. Numer. Anal. , 13 (1976) pp. 172–184 |
| [a4] | A. Hoerl, R. Kennard, "Ridge regression" Technometrics , 12 (1970) pp. 55–82 |
| [a5] | B. Hofmann, "Regularization for applied inverse and ill-posed problems" , Teubner (1986) |
| [a6] | A.K. Louis, "Inverse und schlecht gestellte Probleme" , Teubner (1989) |
| [a7] | M.Z. Nashed, G. Wahba, "Convergence rates of approximate least squares solutions of linear integral and operator equations of the first kind" Math. Comp. , 28 (1974) pp. 69–80 |
| [a8] | J. Varah, "A practical examination of some numerical methods for linear discrete ill-posed problems" SIAM Rev. , 21 (1979) pp. 100–111 |
Regularization method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Regularization_method&oldid=16489