Difference between revisions of "Regularity criteria"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
Ulf Rehmann (talk | contribs) m (Undo revision 48488 by Ulf Rehmann (talk)) Tag: Undo |
||
| Line 1: | Line 1: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
''for summation methods'' | ''for summation methods'' | ||
Conditions for the regularity of [[Summation methods|summation methods]]. | Conditions for the regularity of [[Summation methods|summation methods]]. | ||
| − | For a [[Matrix summation method|matrix summation method]] defined by a transformation of a sequence into a sequence by means of a matrix | + | For a [[Matrix summation method|matrix summation method]] defined by a transformation of a sequence into a sequence by means of a matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080910/r0809101.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080910/r0809102.png" /> the conditions |
| − | |||
| − | the conditions | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080910/r0809103.png" /></td> <td valign="top" style="width:5%;text-align:right;">(1)</td></tr></table> | |
| − | |||
| − | are necessary and sufficient for regularity. For the matrix summation method defined by a transformation of a series into a sequence by means of a matrix | + | are necessary and sufficient for regularity. For the matrix summation method defined by a transformation of a series into a sequence by means of a matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080910/r0809104.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080910/r0809105.png" /> necessary and sufficient conditions for regularity are as follows: |
| − | |||
| − | necessary and sufficient conditions for regularity are as follows: | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080910/r0809106.png" /></td> <td valign="top" style="width:5%;text-align:right;">(2)</td></tr></table> | |
| − | |||
| − | The conditions (1) were originally established by O. Toeplitz [[#References|[1]]] for triangular summation methods, and were then extended by H. Steinhaus [[#References|[2]]] to arbitrary matrix summation methods. In connection with this, a matrix satisfying conditions (1) is sometimes called a Toeplitz matrix or a | + | The conditions (1) were originally established by O. Toeplitz [[#References|[1]]] for triangular summation methods, and were then extended by H. Steinhaus [[#References|[2]]] to arbitrary matrix summation methods. In connection with this, a matrix satisfying conditions (1) is sometimes called a Toeplitz matrix or a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080910/r0809108.png" />-matrix. |
| − | matrix. | ||
| − | For a [[Semi-continuous summation method|semi-continuous summation method]], defined by a transformation of a sequence into a function by means of a semi-continuous matrix | + | For a [[Semi-continuous summation method|semi-continuous summation method]], defined by a transformation of a sequence into a function by means of a semi-continuous matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080910/r0809109.png" /> or a transformation of a series into a function by means of a semi-continuous matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080910/r08091010.png" />, there are regularity criteria analogous to conditions (1) and (2), respectively. |
| − | or a transformation of a series into a function by means of a semi-continuous matrix | ||
| − | there are regularity criteria analogous to conditions (1) and (2), respectively. | ||
A regular matrix summation method is completely regular if all entries of the transformation matrix are non-negative. This condition is in general not necessary for complete regularity. | A regular matrix summation method is completely regular if all entries of the transformation matrix are non-negative. This condition is in general not necessary for complete regularity. | ||
| Line 40: | Line 19: | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> O. Toeplitz, ''Prace Mat. Fiz.'' , '''22''' (1911) pp. 113–119</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> H. Steinhaus, "Some remarks on the generalization of the concept of limit" , ''Selected Math. Papers'' , Polish Acad. Sci. (1985) pp. 88–100</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> G.H. Hardy, "Divergent series" , Clarendon Press (1949)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> R.G. Cooke, "Infinite matrices and sequence spaces" , Macmillan (1950)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> O. Toeplitz, ''Prace Mat. Fiz.'' , '''22''' (1911) pp. 113–119</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> H. Steinhaus, "Some remarks on the generalization of the concept of limit" , ''Selected Math. Papers'' , Polish Acad. Sci. (1985) pp. 88–100</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> G.H. Hardy, "Divergent series" , Clarendon Press (1949)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> R.G. Cooke, "Infinite matrices and sequence spaces" , Macmillan (1950)</TD></TR></table> | ||
| + | |||
| + | |||
====Comments==== | ====Comments==== | ||
Cf. also [[Regular summation methods|Regular summation methods]]. | Cf. also [[Regular summation methods|Regular summation methods]]. | ||
| − | Usually, the phrase [[Toeplitz matrix|Toeplitz matrix]] refers to a matrix | + | Usually, the phrase [[Toeplitz matrix|Toeplitz matrix]] refers to a matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080910/r08091011.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080910/r08091012.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080910/r08091013.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080910/r08091014.png" />. |
| − | with | ||
| − | for all | ||
| − | with | ||
Revision as of 14:53, 7 June 2020
for summation methods
Conditions for the regularity of summation methods.
For a matrix summation method defined by a transformation of a sequence into a sequence by means of a matrix 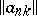 ,
, 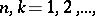 the conditions
the conditions
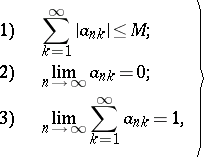 | (1) |
are necessary and sufficient for regularity. For the matrix summation method defined by a transformation of a series into a sequence by means of a matrix 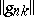 ,
, 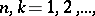 necessary and sufficient conditions for regularity are as follows:
necessary and sufficient conditions for regularity are as follows:
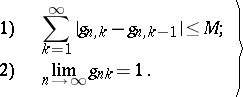 | (2) |
The conditions (1) were originally established by O. Toeplitz [1] for triangular summation methods, and were then extended by H. Steinhaus [2] to arbitrary matrix summation methods. In connection with this, a matrix satisfying conditions (1) is sometimes called a Toeplitz matrix or a 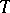 -matrix.
-matrix.
For a semi-continuous summation method, defined by a transformation of a sequence into a function by means of a semi-continuous matrix 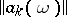 or a transformation of a series into a function by means of a semi-continuous matrix
or a transformation of a series into a function by means of a semi-continuous matrix 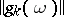 , there are regularity criteria analogous to conditions (1) and (2), respectively.
, there are regularity criteria analogous to conditions (1) and (2), respectively.
A regular matrix summation method is completely regular if all entries of the transformation matrix are non-negative. This condition is in general not necessary for complete regularity.
References
| [1] | O. Toeplitz, Prace Mat. Fiz. , 22 (1911) pp. 113–119 |
| [2] | H. Steinhaus, "Some remarks on the generalization of the concept of limit" , Selected Math. Papers , Polish Acad. Sci. (1985) pp. 88–100 |
| [3] | G.H. Hardy, "Divergent series" , Clarendon Press (1949) |
| [4] | R.G. Cooke, "Infinite matrices and sequence spaces" , Macmillan (1950) |
Comments
Cf. also Regular summation methods.
Usually, the phrase Toeplitz matrix refers to a matrix 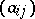 with
with 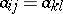 for all
for all 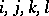 with
with 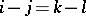 .
.
Regularity criteria. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Regularity_criteria&oldid=48488