Regular summation methods
permanent summation methods
Methods for summing series (sequences) that sum every convergent series (sequence) to the same sum as that to which it converges. Regular summation methods are a special case of conservative summation methods, which sum every convergent series (sequence) to a finite sum, although possibly different from that to which it converges. If a regular summation method is defined by the transformation of a sequence 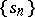 to a sequence
to a sequence 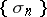 by means of an infinite matrix
by means of an infinite matrix 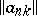 :
:
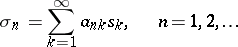 | (*) |
(see Matrix summation method), then the transformation (*) and the matrix of this transformation, 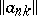 , are called regular.
, are called regular.
Many of the most common summation methods are regular. This applies to the Cesàro summation methods 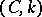 for
for 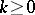 , the Hölder summation methods and the Abel summation method, among others. There are non-regular summation methods, such as the Cesàro summation method
, the Hölder summation methods and the Abel summation method, among others. There are non-regular summation methods, such as the Cesàro summation method 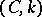 for
for 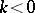 , and the Riemann summation method.
, and the Riemann summation method.
A summation method is called completely regular if it is regular and if it sums every series (sequence) with real terms converging to  (or
(or 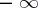 ) to
) to 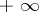 (respectively,
(respectively, 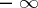 ). A regular summation method defined by a positive matrix is completely regular (see also Regularity criteria).
). A regular summation method defined by a positive matrix is completely regular (see also Regularity criteria).
References
| [1] | G.H. Hardy, "Divergent series" , Clarendon Press (1949) |
| [2] | R.G. Cooke, "Infinite matrices and sequence spaces" , Macmillan (1950) |
| [3] | G.F. Kangro, "Theory of summability of sequences and series" J. Soviet Math. , 5 : 1 (1976) pp. 1–45 Itogi Nauk. i Tekhn. Mat. Anal. , 12 (1974) pp. 5–70 |
| [4] | S. Baron, "Introduction to theory of summation of series" , Tallin (1977) (In Russian) |
Regular summation methods. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Regular_summation_methods&oldid=15873