Regular set function

An additive function defined on a family of sets in a topological space whose total variation (cf. Total variation of a function) satisfies the condition

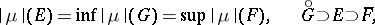where denotes the interior of a set 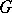and the closure of a set (and , , 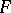are in the domain of definition of 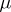). Every bounded additive regular set function, defined on a semi-ring of sets in a compact topological space, is countably additive (Aleksandrov's theorem).

The property of regularity can also be related to a measure, as a special case of a set function, and one speaks of a regular measure, defined on a topological space. For example, the Lebesgue measure is regular.

References

[1]	N. Dunford, J.T. Schwartz, "Linear operators. General theory" , 1 , Wiley (1988)
[2]	A.D. Aleksandrov, "Additive set-functions in abstract spaces" Mat. Sb. , 9 (1941) pp. 563–628 (In Russian)

Comments

Although a set function is called regular if it satisfies a property of approximation from below or above involving "nice" sets, the precise meaning of "regular" usually depends on the context (and on the author). For example, a (Carathéodory) outer measure is called regular if for every part of one has , with a 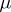-measurable set containing ; if is a topological space, the outer measure 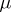is called Borel regular if Borel sets are -measurable and if the above can be taken Borel. On the other hand, if is a metrizable space and is a finite measure on the Borel -field, then is always regular in the sense of the article above. In this setting is often called inner regular, or just regular, if for any Borel subset 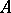one has , with a countable union of compact sets included in , that is, if is a Radon measure. Instead of calling Radon, one nowadays most often says that it is tight.