Regular extremal
non-singular extremal
An extremal  at all points of which the following condition holds:
at all points of which the following condition holds:
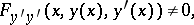 | (1) |
where  is the integrand appearing in a functional
is the integrand appearing in a functional
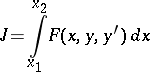 |
which is to be minimized. Like any extremal, a regular extremal is, by definition, a smooth solution of the Euler equation
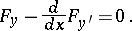 |
The points of an extremal at which (1) holds are called regular points. It is known that at every regular point, an extremal  has a continuous second-order derivative
has a continuous second-order derivative  . On a regular extremal, the second-order derivative
. On a regular extremal, the second-order derivative  is continuous. For a regular extremal the Euler equation
is continuous. For a regular extremal the Euler equation
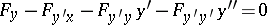 |
can be written in the following form (that is, solved for the highest derivative):
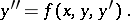 |
The regularity property (1) is directly connected with the necessary Legendre condition (in the strong form), according to which at all points of the extremal the following inequality holds:
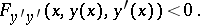 |
Essential use is made of regularity when proving that an extremal 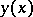 can be included in a field of extremals surrounding it. If condition (1) is violated at even one point, the extremal cannot always be included in a field. This condition for including the extremal in a field is one of the sufficient conditions for being an extremal.
can be included in a field of extremals surrounding it. If condition (1) is violated at even one point, the extremal cannot always be included in a field. This condition for including the extremal in a field is one of the sufficient conditions for being an extremal.
The above definition of a regular extremal is given for the simplest problem of the calculus of variations, which concerns functionals depending on one unknown function. For functionals depending on  unknown functions,
unknown functions,
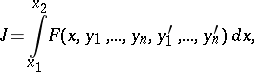 |
a regular extremal is an extremal for which at every point the  -th order determinant
-th order determinant
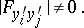 | (2) |
In some general problems of the calculus of variations on a conditional extremum (see Bolza problem), a regular extremal is defined in a similar way, except that in (2) instead of  one must put the Lagrange function
one must put the Lagrange function 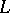 .
.
An extremal for which the regularity condition ((1) or (2)) is violated at every point of some section is called a singular extremal, and the section is called a section of singular regime. For singular regimes there are necessary conditions supplementing the known classical necessary conditions for an extremum (see Optimal singular regime).
References
| [1] | G.A. Bliss, "Lectures on the calculus of variations" , Chicago Univ. Press (1947) |
| [2] | M.A. Lavrent'ev, L.A. Lyusternik, "A course in variational calculus" , Moscow-Leningrad (1950) (In Russian) |
Comments
A family of curves in a domain  is called a field of curves if for every point of
is called a field of curves if for every point of 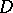 there is exactly one member of the family passing through it. For an account of the role of field theory in the calculus of variations and fields of extremals cf. [a2] and Extremal field.
there is exactly one member of the family passing through it. For an account of the role of field theory in the calculus of variations and fields of extremals cf. [a2] and Extremal field.
References
| [a1] | L. Cesari, "Optimization - Theory and applications" , Springer (1983) |
| [a2] | Yu.P. Petrov, "Variational methods in optimum control theory" , Acad. Press (1968) pp. Chapt. IV (Translated from Russian) |
Regular extremal. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Regular_extremal&oldid=17757