Reflexive space
A Banach space 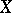 that coincides under the canonical imbedding with its second dual
that coincides under the canonical imbedding with its second dual 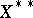 (cf. Adjoint space). More precisely, let
(cf. Adjoint space). More precisely, let  be the space dual to
be the space dual to 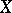 , i.e. the set of all continuous linear functionals defined on
, i.e. the set of all continuous linear functionals defined on 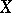 . If
. If 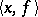 is the value of the functional
is the value of the functional 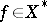 on an element
on an element 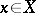 , then with a fixed
, then with a fixed  and
and 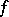 running through
running through 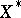 , the formula
, the formula  defines a linear functional on
defines a linear functional on 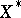 , that is, an element of the space
, that is, an element of the space 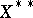 . Let
. Let 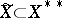 be the set of such functionals. The correspondence
be the set of such functionals. The correspondence 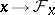 is an isomorphism which does not change the norm:
is an isomorphism which does not change the norm:  . If
. If 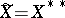 , then the space
, then the space  is called reflexive. The spaces
is called reflexive. The spaces  and
and  ,
, 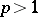 , are reflexive, and the space
, are reflexive, and the space 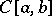 is not reflexive.
is not reflexive.
A space 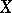 is reflexive if and only if the space
is reflexive if and only if the space 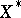 is reflexive. Another criteria of reflexivity of a Banach space
is reflexive. Another criteria of reflexivity of a Banach space 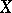 is weak compactness (cf. Weak topology) of the unit ball of this space.
is weak compactness (cf. Weak topology) of the unit ball of this space.
A reflexive space is weakly complete and a closed subspace of a reflexive space is reflexive.
The concept of reflexivity naturally extends to locally convex spaces (cf. Locally convex space).
References
| [1] | N. Dunford, J.T. Schwartz, "Linear operators. General theory" , 1 , Interscience (1958) |
| [2] | K. Yosida, "Functional analysis" , Springer (1980) pp. Chapt. 8, §1 |
| [3] | L.V. Kantorovich, G.P. Akilov, "Functional analysis" , Pergamon (1982) (Translated from Russian) |
Comments
References
| [a1] | B. Beauzamy, "Introduction to Banach spaces and their geometry" , North-Holland (1982) |
| [a2] | M.M. Day, "Normed linear spaces" , Springer (1973) |
| [a3] | D. van Dulst, "Reflexive and superreflexive Banach spaces" , MC Tracts , 102 , Math. Centre (1978) |
Reflexive space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Reflexive_space&oldid=17039