Reducible linear system
From Encyclopedia of Mathematics
of ordinary differential equations
A system
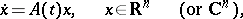 | (*) |
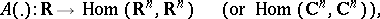 |
that can be transformed into a system 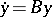 with constant coefficients by a change of variables
with constant coefficients by a change of variables 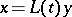 , where
, where 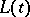 is a Lyapunov transformation. If the mapping
is a Lyapunov transformation. If the mapping 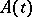 is continuous and periodically depends on
is continuous and periodically depends on 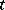 , then (*) is a reducible system (Lyapunov's theorem). The system (*) is reducible if and only if there is a Lyapunov transformation
, then (*) is a reducible system (Lyapunov's theorem). The system (*) is reducible if and only if there is a Lyapunov transformation 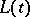 and an operator
and an operator 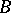 such that every solution of (*) has the form
such that every solution of (*) has the form
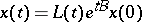 |
(Erugin's criterion).
References
| [1] | A.M. Lyapunov, "Stability of motion" , Acad. Press (1966) (Translated from Russian) |
| [2] | N.P. Erugin, "Reducible systems" Trudy Mat. Inst. Steklov. , 13 (1946) (In Russian) |
How to Cite This Entry:
Reducible linear system. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Reducible_linear_system&oldid=18924
Reducible linear system. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Reducible_linear_system&oldid=18924
This article was adapted from an original article by V.M. Millionshchikov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article