Reduced norm
From Encyclopedia of Mathematics
Let 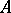 be a finite-dimensional central simple algebra over
be a finite-dimensional central simple algebra over 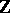 . A finite extension field
. A finite extension field 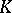 of
of 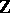 is a splitting field for
is a splitting field for 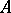 if
if 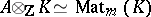 as
as 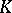 -algebras for some
-algebras for some 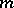 . Here
. Here 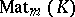 is the
is the 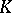 -algebra of
-algebra of 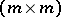 -matrices. Choose an isomorphism
-matrices. Choose an isomorphism 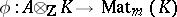 . The reduced norm mapping
. The reduced norm mapping 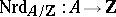 is now defined by
is now defined by
 |
and the reduced trace mapping 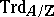 is similarly defined by
is similarly defined by
 |
One checks that the right-hand sides of these equations are indeed in 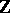 (and not just in
(and not just in 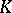 ) and that the definitions are independent of the choices of
) and that the definitions are independent of the choices of 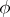 and
and 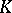 .
.
The reduced norm is multiplicative, and 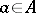 is invertible if and only if
is invertible if and only if 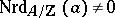 . The reduced trace is a homomorphism of
. The reduced trace is a homomorphism of 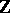 vector spaces, and
vector spaces, and 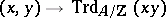 defines a non-degenerate bilinear form on
defines a non-degenerate bilinear form on 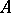 .
.
References
| [a1] | H. Bass, "Algebraic 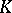 -theory" , Benjamin (1967) pp. 152ff -theory" , Benjamin (1967) pp. 152ff |
| [a2] | A.J. Hahn, O.T. O'Meara, "The classical groups and 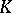 -theory" , Springer (1979) pp. §2.2D -theory" , Springer (1979) pp. §2.2D |
How to Cite This Entry:
Reduced norm. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Reduced_norm&oldid=13357
Reduced norm. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Reduced_norm&oldid=13357