Recursive sequence
From Encyclopedia of Mathematics
recurrent sequence
A sequence  that satisfies a relation
that satisfies a relation
 |
where  are constants. The relation permits one to compute the terms of the sequence one by one, in succession, if the first
are constants. The relation permits one to compute the terms of the sequence one by one, in succession, if the first 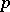 terms are known. A classical example of such a sequence is the Fibonacci sequence
terms are known. A classical example of such a sequence is the Fibonacci sequence  (
( ,
,  ). A recursive series is a power series
). A recursive series is a power series 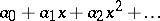 whose coefficients form a recursive sequence. Such a series represents an everywhere-defined rational function.
whose coefficients form a recursive sequence. Such a series represents an everywhere-defined rational function.
Comments
A good reference treating many aspects of such sequences is [a1].
References
| [a1] | A.J. van der Poorten, "Some facts that should be better known, especially about rational functions" R.A. Molin (ed.) , Number theory and applications (Proc. First Conf. Canadian Number Theory Assoc., Banff, April 1988) , Kluwer (1989) pp. 497–528 |
How to Cite This Entry:
Recursive sequence. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Recursive_sequence&oldid=12807
Recursive sequence. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Recursive_sequence&oldid=12807
This article was adapted from an original article by BSE-3 (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article