Recursive realizability
A more precise definition of the intuitionistic semantics of arithmetical formulas, based on the concept of a partial recursive function as proposed by S.C. Kleene (see [1], [2]). For every closed arithmetical formula 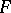 , a relation "the natural number e realizes the formula F" is defined; it is denoted by
, a relation "the natural number e realizes the formula F" is defined; it is denoted by 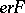 . The relation
. The relation 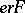 is defined inductively according to the structure of the formula
is defined inductively according to the structure of the formula 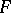 .
.
1) If 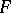 is an atomic formula without free variables, i.e.
is an atomic formula without free variables, i.e. 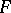 is of the form
is of the form  where
where  and
and 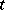 are constant terms, then
are constant terms, then 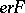 if and only if
if and only if 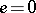 and the values of the terms
and the values of the terms  and
and 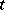 coincide.
coincide.
Let 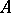 and
and  be formulas without free variables.
be formulas without free variables.
2) 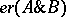 if and only if
if and only if  , where
, where 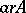 ,
, 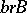 .
.
3) 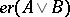 if and only if
if and only if 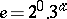 and
and 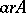 , or
, or 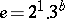 and
and 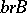 .
.
4) 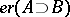 if and only if
if and only if  is the Gödel number of a unary partial recursive function
is the Gödel number of a unary partial recursive function  such that for any natural number
such that for any natural number  ,
, 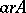 implies that
implies that 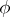 is defined at
is defined at  and
and 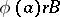 .
.
5) 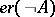 if and only if
if and only if 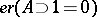 .
.
Let 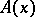 be a formula without free variables other than
be a formula without free variables other than  ; if
; if  is a natural number, then
is a natural number, then 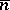 is a term which denotes the number
is a term which denotes the number  in formal arithmetic.
in formal arithmetic.
6) 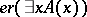 if and only if
if and only if 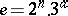 and
and 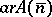 .
.
7)  if and only if
if and only if  is the Gödel number of a recursive function
is the Gödel number of a recursive function 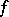 such that for any natural number
such that for any natural number  the number
the number 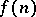 realizes
realizes 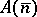 .
.
A closed formula 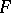 is called realizable if there is a number
is called realizable if there is a number  which realizes
which realizes 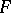 . A formula
. A formula 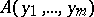 containing the free variables
containing the free variables 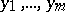 can be regarded as a predicate in
can be regarded as a predicate in 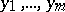 ( "the formula Ay1…ym is realizable" ). If a formula
( "the formula Ay1…ym is realizable" ). If a formula 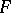 is derivable from realizable formulas in intuitionistic arithmetic, then
is derivable from realizable formulas in intuitionistic arithmetic, then 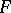 is realizable (see [3]). In particular, every formula which can be proved in intuitionistic arithmetic is realizable. A formula
is realizable (see [3]). In particular, every formula which can be proved in intuitionistic arithmetic is realizable. A formula  can be given for which the formula
can be given for which the formula 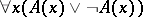 is not realizable. Accordingly, in this case the formula
is not realizable. Accordingly, in this case the formula 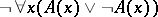 is realizable although it is classically false.
is realizable although it is classically false.
Every predicate formula  which is provable in intuitionistic predicate calculus has the property that each arithmetical formula obtained from
which is provable in intuitionistic predicate calculus has the property that each arithmetical formula obtained from 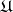 by substitution is realizable. Predicate formulas possessing this property are called realizable. It has been shown [4] that the propositional formula:
by substitution is realizable. Predicate formulas possessing this property are called realizable. It has been shown [4] that the propositional formula:
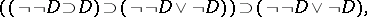 |
where 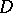 denotes the formula
denotes the formula 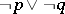 , is realizable but cannot be derived in intuitionistic propositional calculus.
, is realizable but cannot be derived in intuitionistic propositional calculus.
References
| [1] | S.C. Kleene, "On the interpretation of intuitionistic number theory" J. Symbolic Logic , 10 (1945) pp. 109–124 |
| [2] | S.C. Kleene, "Introduction to metamathematics" , North-Holland (1951) |
| [3] | D. Nelson, "Recursive functions and intuitionistic number theory" Trans. Amer. Math. Soc. , 61 (1947) pp. 307–368 |
| [4] | G.F. Rose, "Propositional calculus and realizability" Trans. Amer. Math. Soc. , 75 (1953) pp. 1–19 |
| [5] | P.S. Novikov, "Constructive mathematical logic from a classical point of view" , Moscow (1977) (In Russian) |
Comments
References
| [a1] | M.J. Beeson, "Foundations of constructive mathematics" , Springer (1985) |
| [a2] | D. Mumford, "Abelian varieties" , Oxford Univ. Press (1974) |
Recursive realizability. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Recursive_realizability&oldid=18604