Recursions of higher degrees
Recursive definitions (cf. Recursive definition) that, in addition to numerical functions, use some functions of higher types as auxiliary objects. For example, in the case of recursion of the second degree such are the "substituting" functionals of type
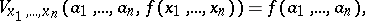 |
as well as functionals that can be obtained from these by this recursion. The interesting property of recursion of higher degree is that multiple recursion can be reduced to single recursion using a transition to a higher degree. This forms the basis for the method of reducing multiple recursions to a normal form. It should be borne in mind that the terminology in this field is not definitely established. In particular, the term "recursions of higher degrees" is sometimes taken to mean normal forms of multiple recursions.
References
| [1] | R. Peter, "Recursive functions" , Acad. Press (1967) (Translated from German) |
Comments
References
| [a1] | S.C. Kleene, "Introduction to metamathematics" , North-Holland (1950) pp. 234 |
| [a2] | P. Odifreddi, "Classical recursion theory" , North-Holland (1989) pp. Chapt. II; esp. pp. 199ff |
Recursions of higher degrees. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Recursions_of_higher_degrees&oldid=17829