Realizability
One of the forms of non-classical interpretation of logical and logico-mathematical languages. Various interpretations of realizability type are defined by the following scheme. For formulas of a logico-mathematical language one defines the relation "an object e realizes a closed formula F" , written "e r F" , for short. The definition is of an inductive nature: The relation 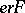 is first defined for atomic formulas
is first defined for atomic formulas 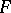 , and then for compound formulas under the assumption that the relation is already defined for the subformulas from which they are made up. A closed formula
, and then for compound formulas under the assumption that the relation is already defined for the subformulas from which they are made up. A closed formula  is called realizable, or true for a given interpretation, if there is an object
is called realizable, or true for a given interpretation, if there is an object  such that
such that  . A formula
. A formula 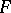 , containing free variables
, containing free variables  , is assumed to be realizable if the closed formula
, is assumed to be realizable if the closed formula  is realizable.
is realizable.
Such an interpretation, known as recursive realizability, was first proposed by S.C. Kleene (see [1], [2]), with the aim of giving an intuitionistic (constructive) semantics of the language of formal arithmetic in terms of recursive functions (cf. Recursive function). Other notions of realizability are modifications of recursive realizability.
The intuitive sense of the relation 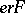 is as follows: The object
is as follows: The object  encodes information from which one can derive the truth of the formula
encodes information from which one can derive the truth of the formula 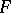 . For example, in recursive realizability, the natural number 0 realizes an elementary formula of the form
. For example, in recursive realizability, the natural number 0 realizes an elementary formula of the form  if and only if this formula is true (i.e. the values of the terms
if and only if this formula is true (i.e. the values of the terms  and
and 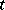 coincide); if a number
coincide); if a number  realizes the disjunction
realizes the disjunction 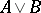 , then
, then  encodes which of the formulas
encodes which of the formulas  or
or 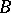 is realizable, and produces a number realizing this formula. If a number
is realizable, and produces a number realizing this formula. If a number  realizes the formula
realizes the formula 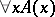 , then
, then  encodes an algorithm which, for any natural number
encodes an algorithm which, for any natural number  , produces a realization of the formula
, produces a realization of the formula 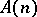 . As realizers, i.e. objects which realize formulas, one can almost always take natural numbers. However, in the intuitionistic interpretation of the language of mathematical analysis, other objects can be used as realizers, such as unary number-theoretical functions (see, for example, [3]).
. As realizers, i.e. objects which realize formulas, one can almost always take natural numbers. However, in the intuitionistic interpretation of the language of mathematical analysis, other objects can be used as realizers, such as unary number-theoretical functions (see, for example, [3]).
For the formulas of a logical language, such as propositional or predicate formulas, realizability is usually defined using the concept of realizability for some logico-mathematical language  . A logical formula
. A logical formula 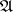 is said to be realizable if every formula in the language
is said to be realizable if every formula in the language  that can be obtained from
that can be obtained from 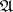 by substituting formulas of
by substituting formulas of  for the predicate variables is realizable.
for the predicate variables is realizable.
Realizability interpretations have found wide application in the study of non-classical, mostly intuitionistic and constructive, logical and logico-mathematical theories. For a description of various notions of realizability and their applications in proof theory for investigations in intuitionistic theories see [3], [4].
References
| [1] | S.C. Kleene, "On the interpretation of intuitionistic number theory" J. Symbolic Logic , 10 (1945) pp. 109–124 |
| [2] | S.C. Kleene, "Introduction to metamathematics" , North-Holland (1951) |
| [3] | S.C. Kleene, R.E. Vesley, "The foundations of intuitionistic mathematics: especially in relation to recursive functions" , North-Holland (1965) |
| [4] | A.G. Dragalin, "Mathematical intuitionism. Introduction to proof theory" , Amer. Math. Soc. (1988) (Translated from Russian) |
Comments
J.M.E. Hyland [a1] has given a "model-theoretic" version of realizability, by showing that it is the internal logic of a certain topos, the effective topos or Hyland realizability topos.
References
| [a1] | J.M.E. Hyland, "The effective topos" A.S. Troelstra (ed.) D. van Dalen (ed.) , The L.E.J. Brouwer Centenary Symposium , North-Holland (1982) pp. 165–216 |
Realizability. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Realizability&oldid=18553