Real-analytic space

An analytic space over the field 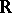of real numbers. Unlike in the case of complex-analytic spaces, the structure sheaves of real-analytic spaces need not be coherent (cf. Coherent sheaf). Real-analytic spaces are said to be coherent if their structure sheaves are coherent. All real-analytic manifolds (i.e. smooth real-analytic spaces) are coherent real-analytic spaces.

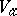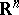Let be the germ at a point of a real-analytic subset of (cf. Analytic set). This defines the germ at of a complex-analytic subset 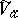of the space 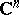with the following equivalent properties: 1) 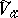is the intersection of all germs of complex-analytic sets containing 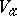; 2) if 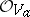is the analytic algebra of the germ 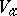, then 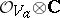is the analytic algebra of the germ 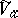. The germ 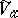is said to be the complexification of the germ 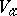, and 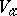is said to be the real part of the germ 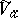. Analogously, for any coherent real-analytic countably-infinite space 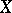it is possible to construct the complexification , which is a complex-analytic space. 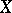will then have a fundamental system of neighbourhoods in 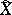which are Stein spaces (cf. Stein space).

The theory of coherent real-analytic spaces is similar to the theory of complex Stein spaces. Global sections of any coherent analytic sheaf of modules 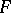on a coherent real-analytic countably-infinite space 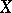generate modules of germs of its sections at any point of 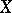, and all groups 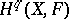vanish if .

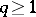For any finite-dimensional coherent real-analytic countably-infinite space 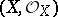there exists a morphism

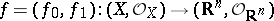such that 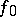is a proper one-to-one mapping of 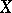into a coherent subspace in 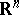, while 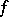is an imbedding at the smooth points of 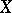. In particular, any (Hausdorff and countably-infinite) real-analytic manifold is isomorphic to a real-analytic submanifold in 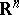. For a reduced coherent real-analytic space 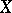the set of classes of isomorphic real-analytic principal fibre bundles with a real structure Lie group 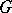, admitting complexification, and base 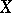is in one-to-one correspondence with the set of classes of isomorphic topological principal fibre bundles with the same structure group .

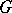References

[1]	A. Tognoli, "Some results in the theory of real analytic spaces" M. Jurchesan (ed.) , Espaces Analytiques (Bucharest 1969) , Acad. Roumanie (1971) pp. 149–157

References

[a1]	H. Cartan, "Variétés analytiques réelles et variétés analytiques complexes" Bull. Soc. Math. France , 85 (1957) pp. 77–99
[a2]	F. Bruhat, H. Cartan, "Sur la structure des sous-ensembles analytiques réels" C.R. Acad. Sci. Paris , 244 (1957) pp. 988–900
[a3]	F. Bruhat, H. Cartan, "Sur les composantes irréductibles d'un sous-ensemble" C.R. Acad. Sci. Paris , 244 (1957) pp. 1123–1126
[a4]	F. Bruhat, H. Whitney, "Quelques propriétés fondamentales des ensembles analytiques-réels" Comm. Math. Helv. , 33 (1959) pp. 132–160
[a5]	R. Narasimhan, "Introduction to the theory of analytic spaces" , Lect. notes in math. , 25 , Springer (1966)
[a6]	H. Grauert, R. Remmert, "Theory of Stein spaces" , Springer (1979) (Translated from German)