Rational tangles
From Encyclopedia of Mathematics
A family of  -tangles (cf. Tangle) classified by J.H. Conway. The
-tangles (cf. Tangle) classified by J.H. Conway. The  -tangle of Fig.a1 is called a rational tangle with Conway notation
-tangle of Fig.a1 is called a rational tangle with Conway notation  . It is a rational
. It is a rational  -tangle if
-tangle if
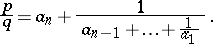 |
The fraction  is called the slope of the tangle and can be identified with the slope of the meridian disc of the solid torus that is the branched double covering of the rational tangle.
is called the slope of the tangle and can be identified with the slope of the meridian disc of the solid torus that is the branched double covering of the rational tangle.

Figure: r130030a
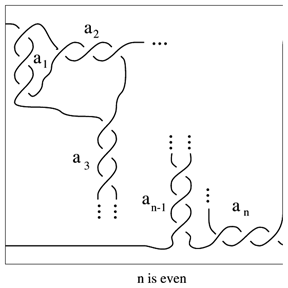
Figure: r130030b
Conway proved that two rational tangles are ambient isotopic (with boundary fixed) if and only if their slopes are equal. A rational  -tangle (also called an
-tangle (also called an  -bridge
-bridge  -tangle) is an
-tangle) is an  -tangle that can be obtained from the identity tangle by a finite number of additions of a single crossing.
-tangle that can be obtained from the identity tangle by a finite number of additions of a single crossing.
References
| [a1] | J.H. Conway, "An enumeration of knots and links" J. Leech (ed.) , Computational Problems in Abstract Algebra , Pergamon Press (1969) pp. 329–358 |
| [a2] | A. Kawauchi, "A survey of knot theory" , Birkhäuser (1996) |
How to Cite This Entry:
Rational tangles. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Rational_tangles&oldid=13459
Rational tangles. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Rational_tangles&oldid=13459
This article was adapted from an original article by Jozef Przytycki (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article