Rational number
A number expressible as a fraction of integers. The formal theory of rational numbers is developed using pairs of integers. One considers ordered pairs  of integers
of integers  and
and 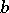 for which
for which 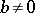 . Two such pairs,
. Two such pairs, 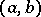 and
and 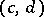 , are called equivalent (equal) if and only if
, are called equivalent (equal) if and only if 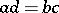 . This is an equivalence relation, being reflexive, symmetric and transitive, and so partitions the set of all such pairs into equivalence classes. A rational number is defined as an equivalence class of pairs. A pair
. This is an equivalence relation, being reflexive, symmetric and transitive, and so partitions the set of all such pairs into equivalence classes. A rational number is defined as an equivalence class of pairs. A pair 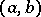 is also called a rational fraction (or fraction of integers). Distinct classes define distinct rational numbers. The set of all rational numbers is countable. The rational number containing a pair of the form
is also called a rational fraction (or fraction of integers). Distinct classes define distinct rational numbers. The set of all rational numbers is countable. The rational number containing a pair of the form 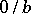 is called zero. If
is called zero. If  is a rational number and
is a rational number and 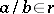 , then the rational number containing
, then the rational number containing 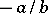 is called the (additive) inverse of
is called the (additive) inverse of  , and is denoted by
, and is denoted by  . A rational number
. A rational number  is called positive (negative) if it contains a rational fraction
is called positive (negative) if it contains a rational fraction 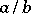 with
with  and
and 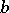 of the same sign (of different signs). If a rational number is positive (negative), then its (additive) inverse is negative (positive). The set of rational numbers can be ordered in the following way: Every negative rational number is less then every positive one, and a positive rational number
of the same sign (of different signs). If a rational number is positive (negative), then its (additive) inverse is negative (positive). The set of rational numbers can be ordered in the following way: Every negative rational number is less then every positive one, and a positive rational number  is less than another positive rational number
is less than another positive rational number 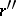 (written
(written 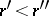 ) if there exist rational fractions
) if there exist rational fractions 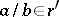 and
and  ,
, 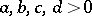 , such that
, such that 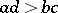 ; every negative (positive) rational number
; every negative (positive) rational number  is smaller (greater) then zero:
is smaller (greater) then zero: 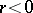 (
(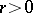 ); a negative rational number
); a negative rational number 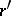 is less than another negative rational number
is less than another negative rational number 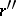 if the positive rational number
if the positive rational number 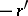 is greater than the positive rational number
is greater than the positive rational number 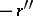 :
: 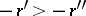 . The absolute value
. The absolute value  of a rational number
of a rational number  is defined in the usual way:
is defined in the usual way:  if
if 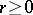 and
and 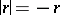 if
if 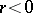 .
.
The sum of two rational fractions 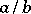 and
and 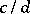 is defined as the rational fraction
is defined as the rational fraction 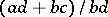 and the product as
and the product as 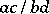 . The sum and product of two rational numbers
. The sum and product of two rational numbers  and
and  are defined as the equivalence classes of rational fractions containing the sum and product of two rational fractions
are defined as the equivalence classes of rational fractions containing the sum and product of two rational fractions 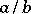 and
and 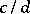 belonging to
belonging to 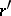 and
and 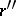 , respectively. The order, sum and product of rational numbers
, respectively. The order, sum and product of rational numbers 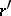 and
and 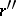 do not depend on the choice of representatives of the corresponding equivalence classes, that is, they are uniquely determined by
do not depend on the choice of representatives of the corresponding equivalence classes, that is, they are uniquely determined by  and
and 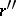 themselves. The rational numbers form an ordered field, denoted by
themselves. The rational numbers form an ordered field, denoted by 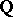 .
.
A rational number  is denoted by any rational fraction
is denoted by any rational fraction 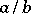 from its equivalence class, i.e.
from its equivalence class, i.e.  . Thus, one and the same rational number can be written as distinct, but equivalent, rational fractions.
. Thus, one and the same rational number can be written as distinct, but equivalent, rational fractions.
If every rational number containing a rational fraction of the form 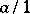 is associated with the integer
is associated with the integer  , then one obtains an isomorphism from the set of such rational numbers onto the ring
, then one obtains an isomorphism from the set of such rational numbers onto the ring  of integers. Therefore, the rational number containing a rational fraction of the form
of integers. Therefore, the rational number containing a rational fraction of the form 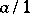 is denoted by
is denoted by  .
.
Each function of the form
 | (1) |
is a norm on the field of rational numbers 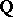 , that is, it satisfies the conditions:
, that is, it satisfies the conditions:
1) 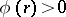 for any
for any 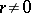 ,
, 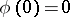 ;
;
2) 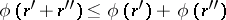 ;
;
3) 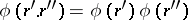 for all
for all 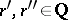 . The field of rational numbers is not complete with respect to the norm (1). The completion of
. The field of rational numbers is not complete with respect to the norm (1). The completion of 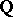 with respect to the norm (1) yields the field of real numbers.
with respect to the norm (1) yields the field of real numbers.
Consider the function
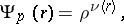 | (2) |
where 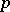 is a prime number,
is a prime number,  is a rational number and
is a rational number and 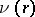 is determined by:
is determined by:
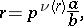 |
where 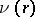 is an integer,
is an integer, 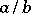 is an irreducible rational fraction such that
is an irreducible rational fraction such that  and
and 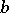 are not divisible by
are not divisible by 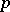 , and
, and  is a fixed number,
is a fixed number, 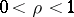 . Then
. Then  is a norm on
is a norm on  . It induces the so-called
. It induces the so-called 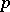 -adic metric.
-adic metric.  is not complete with respect to this metric. By completing
is not complete with respect to this metric. By completing 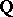 with respect to the norm (2), one obtains the field of
with respect to the norm (2), one obtains the field of 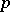 -adic numbers (cf.
-adic numbers (cf.  -adic number). The metrics induced by (1) and (2) (for all prime numbers) exhaust all non-trivial metrics on
-adic number). The metrics induced by (1) and (2) (for all prime numbers) exhaust all non-trivial metrics on 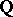 .
.
In decimal notation, only rational numbers are representable as periodic decimals fractions.
References
| [1] | Z.I. Borevich, I.R. Shafarevich, "Number theory" , Acad. Press (1987) (Translated from Russian) (German translation: Birkhäuser, 1966) |
| [2] | C. Pisot, M. Zamansky, "Mathématiques générales: algèbre-analyse" , Dunod (1966) |
Comments
Another property characterizing rational numbers is that their continued fraction is finite. A very important theme in number theory is to find only the rational solutions of equations such as 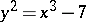 ,
, 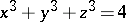 , etc. (see Diophantine equations). Finally, the subject of "rational numbers" is intimately connected with that of irrational numbers (cf. Irrational number). It is not known, for example, whether or not
, etc. (see Diophantine equations). Finally, the subject of "rational numbers" is intimately connected with that of irrational numbers (cf. Irrational number). It is not known, for example, whether or not 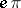 ,
, 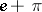 or the Euler constant
or the Euler constant 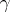 are rational.
are rational.
References
| [a1] | G.H. Hardy, E.M. Wright, "An introduction to the theory of numbers" , Oxford Univ. Press (1979) pp. Chapt. XIII |
| [a2] | G. Bachman, "Introduction to 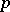 -adic numbers and valuation theory" , Acad. Press (1964) -adic numbers and valuation theory" , Acad. Press (1964) |
| [a3] | B.L. van der Waerden, "Algebra" , 2 , Springer (1971) (Translated from German) |
Rational number. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Rational_number&oldid=14864